비전공자의 인공지능 고군분투기

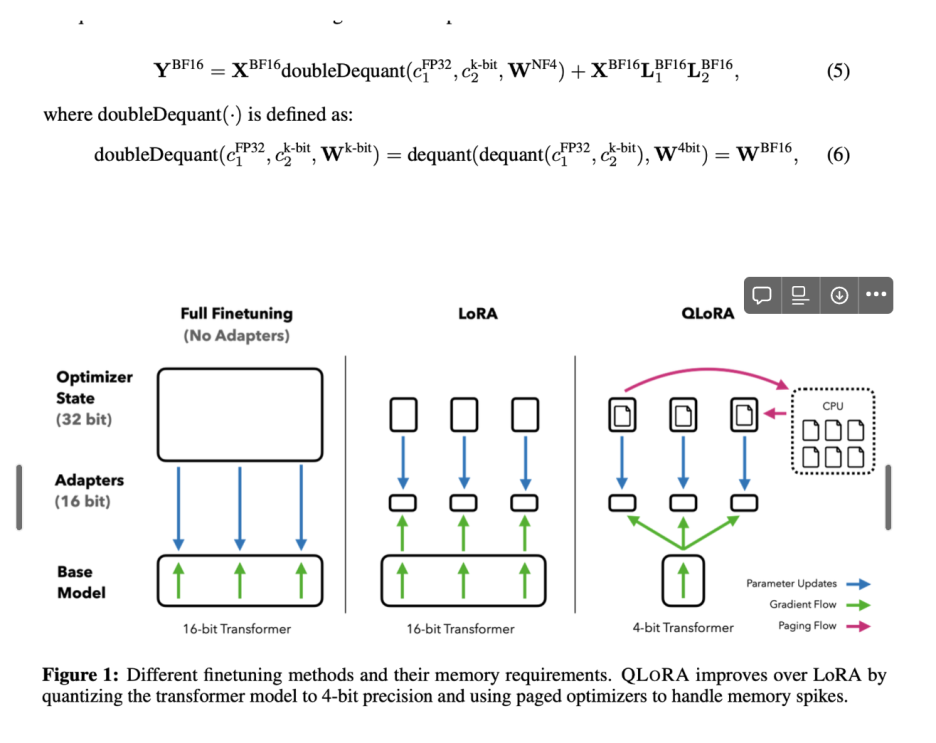
안녕하세요,  오늘은 QLoRA (Quantized Low-Rank Adapter) 에 대해 간단하게 리뷰해보도록 하겠습니다.QLoRA는 파라미터 효율적 미세 조정(PEFT, Parameter-Efficient Fine-Tuning)을 위한 방법 중 하나로, 대형 언어 모델(LLM)을 저비용으로, 더 적은 자원으로 미세 조정하기 위해 설계되었습니다. 특히 FP4(4-bit 부동소수점) 양자화와 낮은 Rank 어댑터(Low-Rank Adapter)를 결합하여 효율성과 성능을 극대화합니다. 그렇다면, LoRA와 QLoRA의 차이가 무엇일까요? LoRA는 기존 모델의 일부 파라미터만 저랭크 형태로 미세 조정하여 메모리와 연산 비용을 줄이는 방법이고,QLoRA는 LoRA에 4비트 양자화를 추가하여 더 적은 메모..

안녕하세요, 오늘은 MIT 선형대수(Linear algebra) 5강 Transposes, permutations, vector spaces에 대해 학습해보겠습니다.   Permutations(치환)Multiplication by a permutation matrix치환행렬은 행교환 (row exchange)을 수행하는 행렬이다. 행교환은 pivot이 0인 경우에 반드시 필요하다. P swaps the rows of a matrix; when applying the method of elimination we use permutation matrices to move ze­ros out of pivot positions. Our factorization A = LU then becomes PA = LU,..

안녕하세요,  오늘은 Computer Vision 논문리뷰를 해보려고 합니다. 비전공자이다보니까 수식이 어떻게 활용되었는지 논문을 읽을때마다 어렵기도 하고, 어려운 부분인 것 같아요.제가 다룰 논문 리뷰들에서는 어떻게 수식이 적용되었는지 보여드릴 예정이니 비전공이신분들도 두려워마시고 차근차근 읽어서 가져가시기 바랍니다. Multimodal에 관한 연구를 하시는 분들에게 조금이나마 도움이 되시기 바랍니다.  DreamBooth: Fine Tuning Text-to-Image Diffusion Models for Subject-Driven Generation ( Ruiz, N., Li, Y., Jampani, V., Pritch, Y., Rubinstein, M., & Aberman, K. CVPR 2023..

안녕하세요, 오늘은 MT Gilbert Strang 교수님의 Linear Algebra 수업 Lecture4, Factorization into A = LU 에 대해 다루어보겠습니다.      Inverse of a productThe inverse of a matrix product AB is B−1 A−1. AB의 역행렬은 B−1 A−1이다.  Transpose of a product행과 열을 바꿀 때 사용the entry in row i column j of A is the entry in row j column i of A^T열I와 행J의 A를 열J와 행I으로 바꾼 것을 A^T라고 한다. The transpose of a matrix product AB is BTAT. For any invert..

안녕하세요 오늘은 MIT Gilbert Strang교수님의 Linear algebra 3강 Multiplication and Inverse Matrices를 공부하도록 하겠습니다. Matrix A multiplying 1. Column Combination행*열의 곱을 원소별 계산으로 정리할 수 있다. (대부분은 벡터로 표현)If they are square, they have got to be the same.If they are rectangular, they are not the same size.here goes A, again, times B producing C.A times a vector is a combination of the columns of A.because the columns ..

안녕하세요, 오늘은 MIT Gilbert Strang교수님의 선형대수 강의 Lecture#2 Elimination with Matrices로 공부해보도록 하겠습니다.  Method of EliminationElimination is the technique most commonly used by computer software to solve systems of linear equations. It finds a solution x to Ax = b whenever the matrix A is invertible. In the example used in class,The number 1 in the upper left corner of A is called the first pivot.The first..

안녕하세요, 인공지능 전공자라면 정말 중요하지만 어렵게 느끼는 선형대수학 입니다. 오늘은 MIT GilbertStrang 교수님의 2강인 An Overview of Linear Algebra 에 대해 리뷰해보겠습니다.   This is an overview of linear algebra given at the start of a course on the math­ ematics of engineering.  VectorsWhat do we do with vectors? Take combinationsWe can multiply vectors by scalars(such as under x1,x2,x3), add, and subtract. Given vectors u, vand w we can form ..

안녕하세요, 오늘은 최근에 읽은 채근담 철학노트 필사본에 대해 간략 리뷰하고자 합니다. 채근담은 동양의 탈무드라는 말이 있듯이, 지혜롭계 사람과의 관계를 맺고 어떻게 하면 군자가 될 수 있는지에 다룬 책입니다. 읽기에 어렵다는 말들도 있으나 제가 읽은 아래의 책은 책은 두껍지 않아 읽기에 편했습니다. 여러 좋은 글귀들이 있었으나, 저는 6장 군자의 도리에 따른다는 것 부분이 가장 좋았습니다. 부귀영화를 가까이하지 않는 이도 청렴결백하지만, 가까이하면서도 물들지 않는 사람이 더욱 고결한 사람이다.권모술수를 모르는 이도 뛰어나지만, 쓸 줄 알면서도 쓰지 않는 사람이 더욱 뛰어난 사람이다.  부귀영화를 가까이하면서 물들지 않는 사람, 권모술수를 알면서 쓰지 않는 사람이 되기란 참 어렵죠,그래서 6장에서는 이러..

안녕하세요, 오늘은 대학원 입학 전에 참여하였던 Deep daiv에서 다루었던 논문인 ReACT에 대해 리뷰해보도록 하겠습니다. REACT: SYNERGIZING REASONING AND ACTING IN LANGUAGE MODELS   ReACT언어모델은 추론과 실행에서 좋아지고 있지만, 두가지 방향은 여전히 분리되어 있다.ReACT는 두가지 기본 기능을 결합하면 어떻게 되는지를 보여준다. AbstractLLM은 언어를 이해하고 대화형 의사결정 작업 전반에 걸쳐 좋은 기능을 보여주었지만 추론 및 실행은 주로 별도의 주제로 연구되었다. 본 문서에서는 추론 추적과 작업별 작업을 interleaved 방식으로 생성하기 위해 LLM을 사용하여 둘 사이의 큰 시너지 효과를 허용하는 방법을 살펴본다.Interle..

안녕하세요,  에피소드2에서는 포스코 AI.Big data 프로그램에 대해 설명을 드렸다면 이번 에피소드3 에서는 서류와 준비과정에 대해 적어보도록 하겠습니다.  POSCO AI.Big DATA 서류합격저는 2023년 4월 17일부터 7월 7일까지 진행하는 22기 과정에 지원하였습니다.사이트 https://youth.posco.com/posco/edu/index.php?mod=academy&pag=academy01 에서 서류접수를 하였고,서류 결과의 경우 아래(그림1)와 같이 3월 31일 금요일 아침에 서류합격 메일을 받았습니다. 내용에는 2단계 면접에 대한 안내사항이 적혀있습니다.시험은 오프라인 시험과 면접을 포항공과대학교 인공지능연구원에서 본다고 하네요.   POSCO AI.Big DATA 시험 및 ..