안녕하세요 오늘은 MIT Gilbert Strang교수님의 Linear algebra 3강 Multiplication and Inverse Matrices를 공부하도록 하겠습니다.

Matrix A multiplying
1. Column Combination
행*열의 곱을 원소별 계산으로 정리할 수 있다. (대부분은 벡터로 표현)


If they are square, they have got to be the same.
If they are rectangular, they are not the same size.
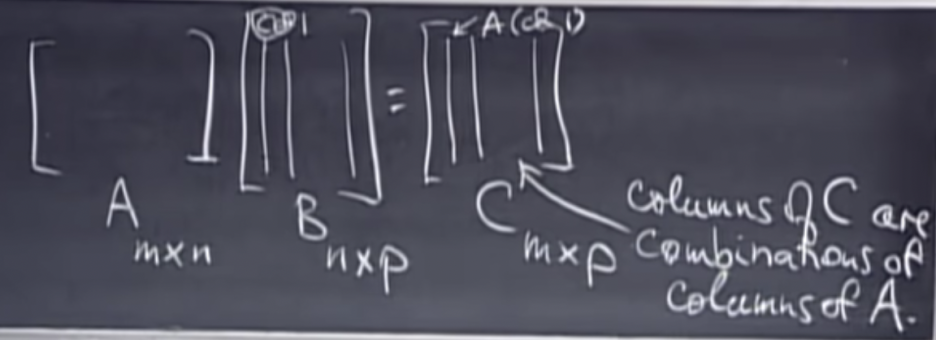
here goes A, again, times B producing C.
A times a vector is a combination of the columns of A.
because the columns of A have length m and the columns of C have lengh m.
Every column of C is some combination of the columns of A.
Columns of C are combinations of columns of A.
앞의 2강의 내용인 column * matrix = column인 것처럼
A와B행렬 각 열의 곱의 조합으로 C라는 새로운 행렬이 나올 수 있다.
즉, 행렬 C의 열(Columns)들은 행렬A의 열(Columns)들의 결합이다.
2. Row Combination
A와B행렬 각 행의 곱의 조합으로 C라는 새로운 행렬이 나올 수 있다.

rows of C are combinations of rows of B.
행렬 C의 행(rows)들은 B행(rows)들의 결합이다.
3. Column * row (행과 열의 곱)

4. Vector combination
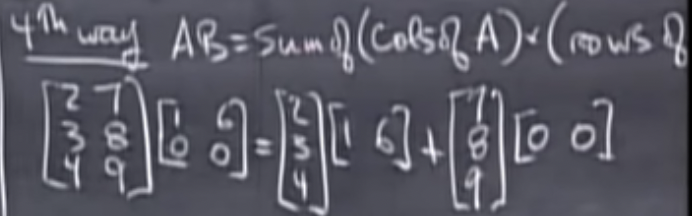
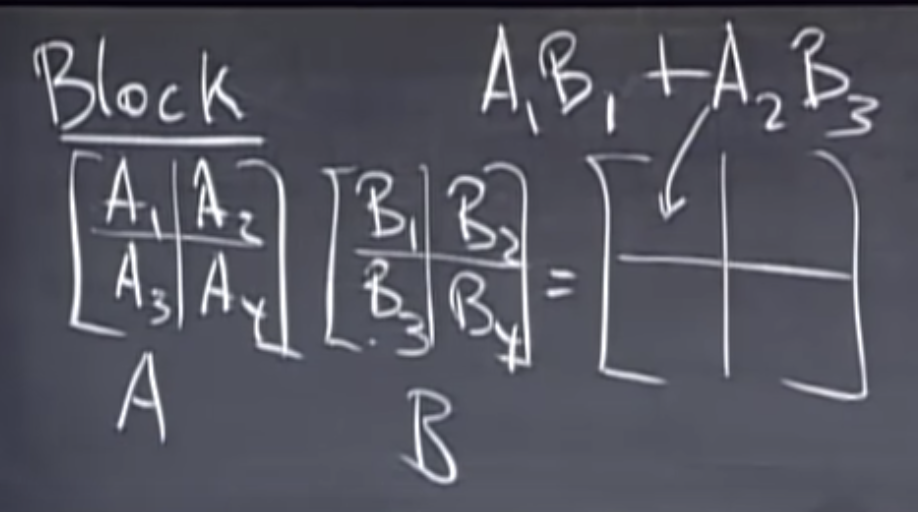
Inverse Matrix(Square Matrices)

A-1은 invertible or non-singular라 불린다.
Singular case
No inverse
두 열은 선형 독립이 아닌 선형 결합이므로 행렬 A는 역행렬이 존재하지 않는다.
즉, Ax=0이 되는 x가 0 밖에 없을 때에만 역행렬이 존재한다.

위의 경우에 (1*3)+(3*-1) = 0 , (2*3)+(6*-1) = 0

Gauss-Jordan
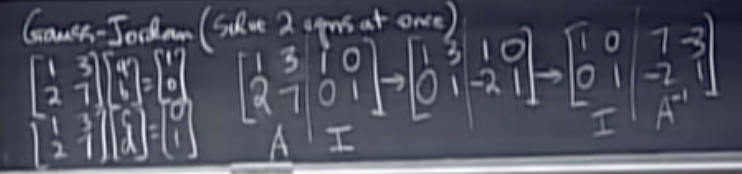
We do row reduction, we do elimination on this long matrix

E times A is I
E must be, EA=I tells us E = A^-1
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture5 Transposes, Permutations, Vector Spaces (2) | 2024.11.26 |
|---|---|
| Lecture #4 Factorization into A = LU (0) | 2024.11.24 |
| Lecture #2. Elimination with Matrices (1) | 2024.11.22 |
| An Overview of Linear Algebra (2) | 2024.11.21 |
| 1. The Geometry of Linear Equations (1) | 2024.11.16 |