안녕하세요,
오늘은 MT Gilbert Strang 교수님의 Linear Algebra 수업 Lecture4, Factorization into A = LU 에 대해 다루어보겠습니다.

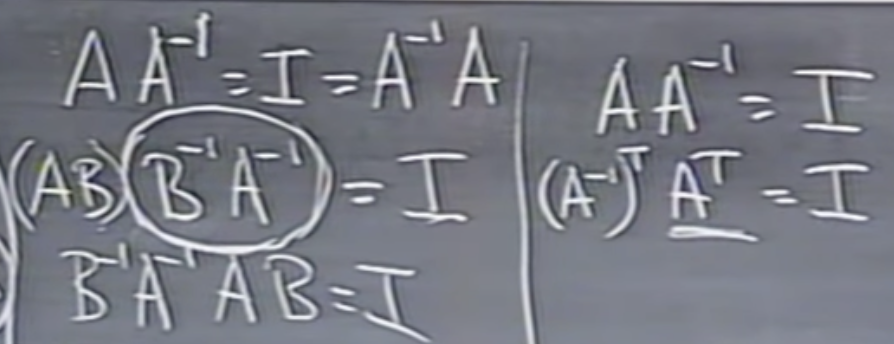
Inverse of a product
The inverse of a matrix product AB is B−1 A−1.
AB의 역행렬은 B−1 A−1이다.
Transpose of a product
행과 열을 바꿀 때 사용
the entry in row i column j of A is the entry in row j column i of A^T
열I와 행J의 A를 열J와 행I으로 바꾼 것을 A^T라고 한다.
The transpose of a matrix product AB is BTAT. For any invertible matrix A, the inverse of A^T is (A−1)^T.
AB의 matrix를 뒤바꾸면 BTAT. AT의 역행렬을 (A^-1)^T.
A = LU
We’ve seen how to use elimination to convert a suitable matrix A into an upper triangular matrix U. This leads to the factorization A = LU, which is very helpful in understanding the matrix A.
우리는 소거법을 사용하여 적합한 행렬 A를 상위 삼각 행렬 U로 변환하는 방법을 살펴보았다. 이는 행렬 A를 이해하는 데 매우 도움이 되는 인수분해 A = LU로 이어진다.
Recall that (when there are no row exchanges) we can describe the elimination of the entries of matrix A in terms of multiplication by a succession of elimination matrices Eij, so that A → E21A → E31E21A → ··· → U. In the two by two case this looks like:
상삼각행렬을 구해보는 과정을 적어보겠다.
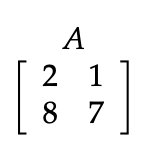
우선 2행의 피봇을 제외하고 첫번째 원소를 0으로 만든다.

행렬로 나타내면 위와 같은 결과가 나온다.
E21과A를 연산하면 1*2 해서 2, 1*1해서 1, -4*2+8해서 0, -4*1+1*7해서3 이라는 U값이 나온다.
A → E21A → E31E21A → ··· → U.
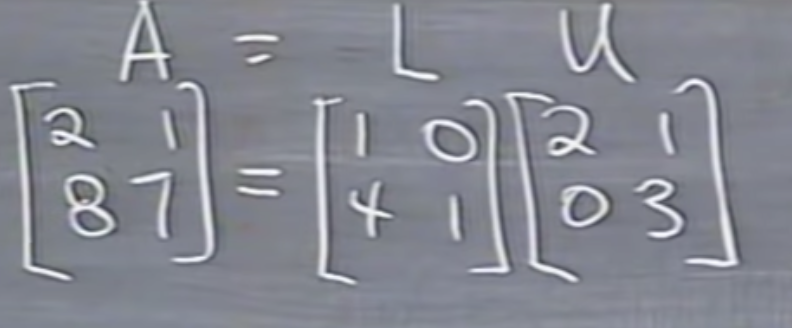
We can convert this to a factorization A = LU by “canceling” the matrix E21; multiply by its inverse to get E−1E21A = E−1U.
행렬 E21을 "canceling"함으로써 인수분해 A = LU로 변환할 수 있다; E-1E21A = E-1U를 얻기 위해 그 역을 곱한다.
즉, (E21)-1을 구하면, A=LU형태를 구할 수 있다.
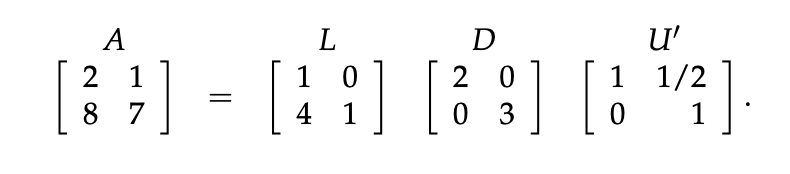
The matrix U is upper triangular with pivots on the diagonal. The matrix L is lower triangular and has ones on the diagonal. Sometimes we will also want to factor out a diagonal matrix whose entries are the pivots:
또한, U행렬을 pivot만 남기고 다시 계산하고자 분해한다면 위와 같이 Diagonal Matrix를 추가로 곱해주면 되고,
이를 LDU라고 한다.
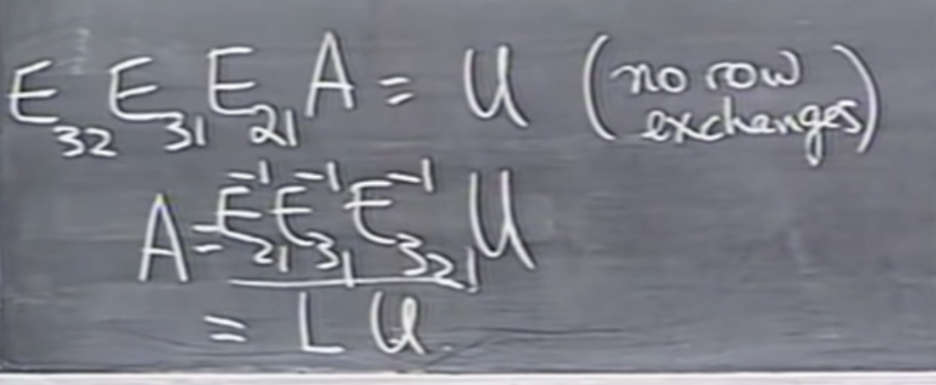
In the three dimensional case, if E32E31E21A = U then A = E−1E−1E−1U = LU.
3*3행렬로 U와 같은 형태와 LU의 형태로 나타낼 수 있다.
For example, suppose E31 is the identity matrix and E32 and E21 are as shown below:
이것에 대한 예는 아래와 같다.

The 10 in the lower left corner arises because we subtracted twice the first row from the second row, then subtracted five times the new second row from the third.
10은 우리가 두 번째 행에서 첫 번째 행의 두 배를 뺐기 때문에 발생하고, 세 번째 행에서 새로운 두 번째 행의 5배를 뻬는 등의 연산을 수행한다. 하지만 이는 효율적이지 못한 다소 불편한 상황이된다.
만약 아래와 같이 역행렬을 구해서 A=LU형태로 구한다면 E32E21행렬의 형태보다 단순화된 행렬이 나타난다.
즉, EA = U는 A=LU보다 효율적이지 않다. 왜냐하면 E를 사용함으로써 추가 계산 비용이 발생하기 때문이다.
LU 분해는 A에 행연산을 직접 적용하여 U를 얻는데 이것이 E를 통해 간접적으로 연산을 적용하는 것보다 더 효율적이다.
*수치 알고리즘과 애플리케이션에는 단순성과 계산 효율성으로 인해 A = LU가 더 선호된다.
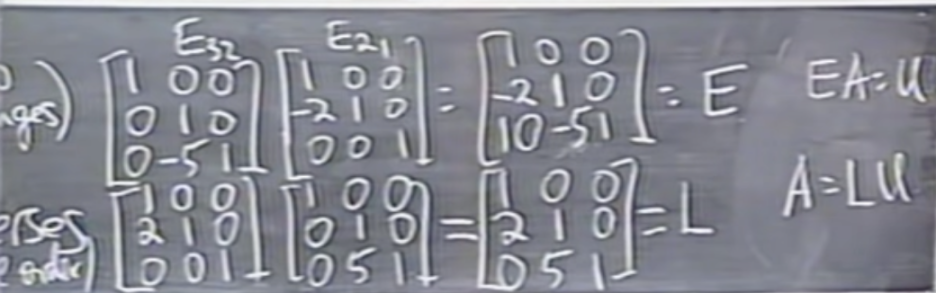
다음으로는 row exchange까지 수행하는 것을 배워보려 한다.


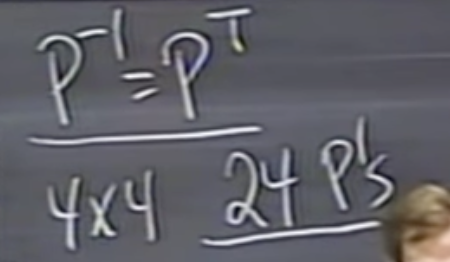
Permutations (치환)을 사용하여 행 바꿈을 시행한다.
3*3 행렬은 총 6가지 치환행렬을 구할 수 있다.
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture6 Column Space and Nullspace (2) | 2024.11.30 |
|---|---|
| Lecture5 Transposes, Permutations, Vector Spaces (2) | 2024.11.26 |
| Lecture#3 Multiplication and Inverse Matrices (0) | 2024.11.23 |
| Lecture #2. Elimination with Matrices (1) | 2024.11.22 |
| An Overview of Linear Algebra (2) | 2024.11.21 |