안녕하세요,
오늘은 MIT Gilbert Strang교수님의 선형대수 강의 Lecture#2 Elimination with Matrices로 공부해보도록 하겠습니다.

Method of Elimination
Elimination is the technique most commonly used by computer software to solve systems of linear equations. It finds a solution x to Ax = b whenever the matrix A is invertible.
In the example used in class,

The number 1 in the upper left corner of A is called the first pivot.
The first number in the second row becomes 0.
The next step is to perform another elimination to get a 0 in row 3 column 1.
The second pivot is the value 2 which now appears in row 2 column 2. We find a multiplier (in this case 2) by which we multiply the second row to elimi nate the 4 in row 3 column 2. The third pivot is then the 5 now in row 3 column 3.
행렬의 Main diagonal(주대각선)을 중심으로 first pivot부터 last pivot의 숫자만을 남기면서
Main diagonal 아래 성분을 0으로 계산해 간다..


We started with an invertible matrix A and ended with an upper triangular matrix U; the lower left portion of U is filled with zeros. Pivots 1, 2, 5 are on the diagonal of U.
행렬 A에서 Upper Triangle Matrix(U)로 선형변환을 이룰 수 있다.
Elimination Matrices
1. Column operation

The result of multiplying a matrix by some vector is a combination of the columns of the matrix.
3 times the first column
3 times column1 + 4 times column2 + 5 times column3.
What this means is that column * matrix = column (Matrix times a column is a column)
열과 행렬의 연산은 열에 대한 연산을 의미한다.
* Q: why the professor emphasize the parallel thing with rows?
A: all operations here for this two weeks of the course are row operations.
2. Row operation

A row times a matrix. and What is the answer?
it is combining the rows and we have a combination, a linear combination of the rows.
What this means is that row * matrix = row
행과 행렬의 연산은 행에 대한 연산을 의미한다.
3.Matricies


The elimination matrix used to eliminate the entry in row m column n is denoted Emn. The calculation above took us from A to E21 A. The three elimination steps leading to U were: E32(E31(E21A)) = U, where E31 = I. Thus E32(E21A) = U.
Matrix multiplication is associative, so we can also write (E32E21)A = U.
The product E32E21 tells us how to get from A to U. The inverse of the matrix E32E21 tells us how to get from U to A.
If we solve Ux = EAx = Eb, then it is also true that Ax = b. This is why the method of elimination works: all steps can be reversed.
4. permutation matrix exchange two rows of a matrix
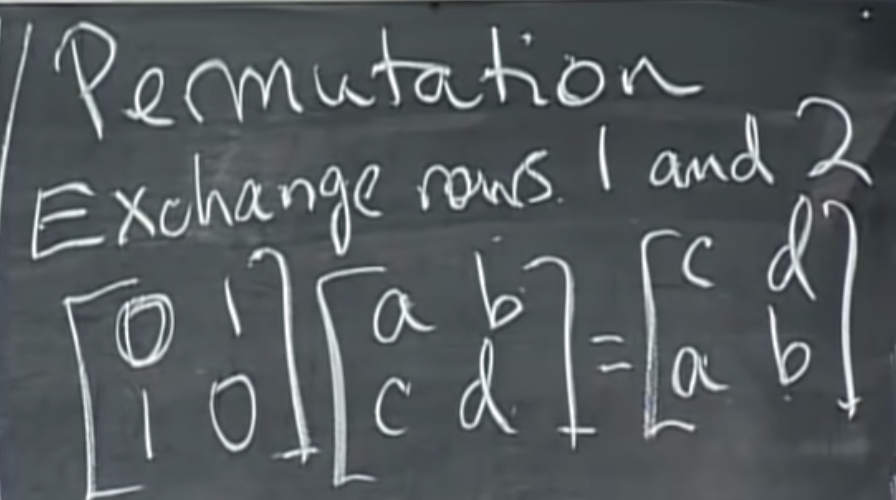
A times B is not the same as B times A
Inverses
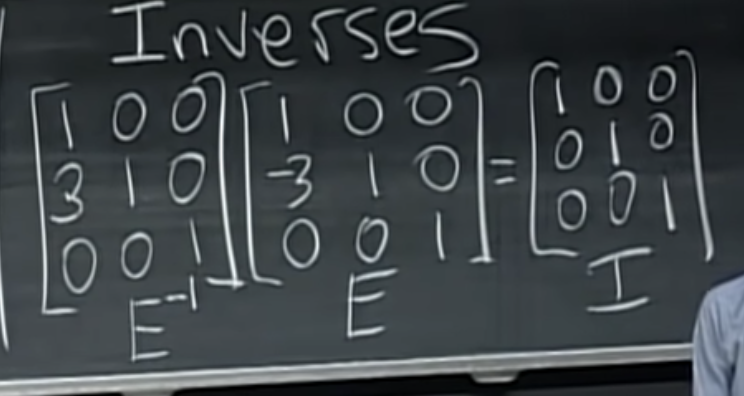
change row two by subtracting 3 of row one.
conclution : E^-1 E = I
감사합니다.
다음에는 3강 리뷰로 돌아오겠습니다.
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture5 Transposes, Permutations, Vector Spaces (2) | 2024.11.26 |
|---|---|
| Lecture #4 Factorization into A = LU (0) | 2024.11.24 |
| Lecture#3 Multiplication and Inverse Matrices (0) | 2024.11.23 |
| An Overview of Linear Algebra (1) | 2024.11.21 |
| 1. The Geometry of Linear Equations (1) | 2024.11.16 |