안녕하세요,
오늘은 MIT 선형대수(Linear algebra) 5강 Transposes, permutations, vector spaces에 대해 학습해보겠습니다.

Permutations(치환)
Multiplication by a permutation matrix
치환행렬은 행교환 (row exchange)을 수행하는 행렬이다. 행교환은 pivot이 0인 경우에 반드시 필요하다.
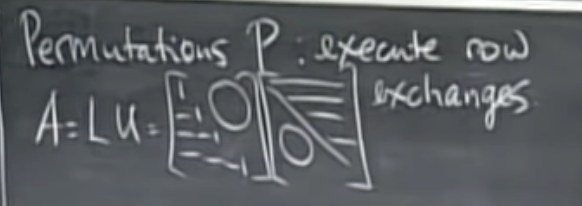

P swaps the rows of a matrix; when applying the method of elimination we use permutation matrices to move zeros out of pivot positions. Our factorization A = LU then becomes PA = LU, where P is a permutation matrix which reorders any number of rows of A. Recall that P−1 = PT, i.e. that PTP = I.
치환행렬 P에 의한 곱셈은 행렬의 행을 교환한다. 제거 방법을 적용할 때, 치환행렬을 사용하여 0을 피벗 위치 밖으로 이동한다.
인수분해 A = LU는 PA = LU가 된다. 여기서 P는 A의 행을 재정렬하는 치환행렬이다. (P−1 = PT, 즉 PTP = I)
P excute row exchanges. (P는 행교환을 시행한다.)


n!는 치환행렬이 가능한 경우의 수이다.
모든 n*n 치환을 counts한다.
치환행렬(permutation)의 속성 3가지
- Excute the row exchanges = n! (n = row)
- 모든 p 행렬은 invertible *역행렬이 존재
- P행렬의 역행렬 = Transpose(전치) 행렬
Transposes(전치)

When we take the transpose of a matrix, its rows become columns and its columns become rows. If we denote the entry in row i column j of matrix A by Aij, then we can describe AT by: (AT)ij =Aji
행렬을 전치하면, rows는 columns이 되고, columns는 rows가 된다. 행렬 A의 i행 j열에 있는 항목을 Aij로 표시하면 AT를 다음과 같이 설명할 수 있다. (AT)ij =Aji
*Symmetric matrices : AT = A (특정행렬에 전치행렬을 곱할 경우 항상 대칭행렬이 된다.)

왜? 행렬*전치행렬은 전치하여도 항상 똑같기 때문이다!
Vector spaces(벡터공간)
벡터의 공간임을 인정받기 위한 3가지 충족조건
1. 벡터 공간 내에 존재하는 임의의 벡터 v와 w는 그 둘을 더해도 (v+w) 그 결과가 반드시 같은 벡터 공간에 존재해야 한다.
2. 벡터 공간 내에 존재하는 임의의 벡터 v에 임의의 상수 c를 곱해도 (cv) 그 결과가 반드시 같은 벡터 공간에 존재해야 한다.
3. 벡터 공간 내에 존재하는 임의의 벡터 v, w와 임의의 상수 c, d에 대해 모든 경우의 cv+dw 조합(각 벡터에 임의의 상수를 곱한 뒤 더하는, 즉 선형 결합(Linear Combination))결과가 반드시 같은 벡터 공간에 존재해야 한다.

We can add vectors and multiply them by numbers, which means we can dis cuss linear combinations of vectors. These combinations follow the rules of a vector space.
모든 형태의 벡터는 다른 벡터의 합과 곱으로 표현될 수 있다. 이러한 조합은 벡터 공간의 규칙을 따른다.
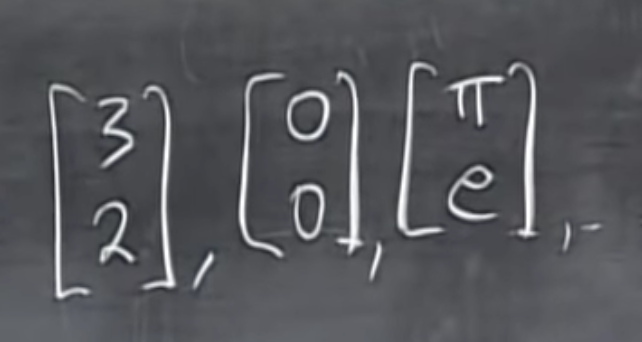


Subspace(부분공간) : 원점을 통과한 R^2에 속한 벡터
같은 공간에 있는 벡터들은 동일한 공간에 존재하는 다른 벡터들의 선형 결합에 의해 정의될 수 있어야 한다.
A line in R2 that does not pass through the origin is not a subspace of R2.
Multiplying any vector on that line by 0 gives the zero vector, which does not lie on the line. Every subspace must contain the zero vector because vector spaces are closed under multiplication.
원점을 통과하지 않는 R2의 선은 R2의 부분공간이 아니다.
해당 선의 벡터에 0을 곱하면 선에 있지 않은 0 벡터가 됩니다. 벡터 공간은 곱셈에 따라 닫혀 있으므로 모든 부분 공간에는 0 벡터가 포함되어야 한다.
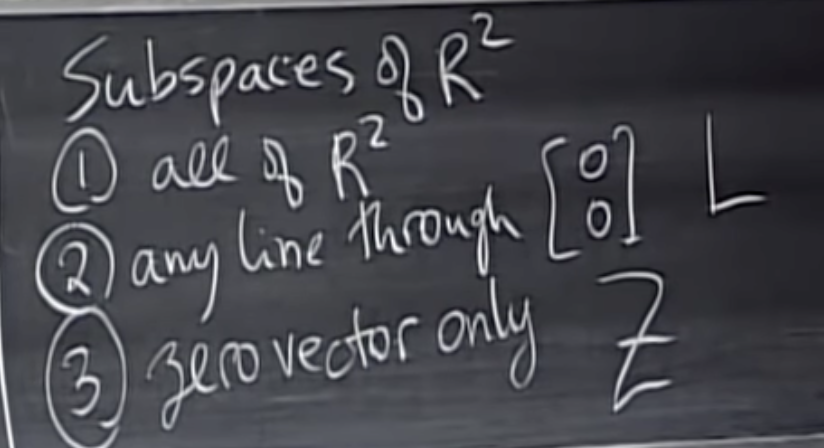
R2의 부분집합
1) 모든 R^2
2)[0,0]을 통과하는 모든 라인
3) 제로벡터

R^3의 모든 부분집합
1)모든 R^3
2) 원점을 통과하는 모든 plane과 line
3)제로벡터

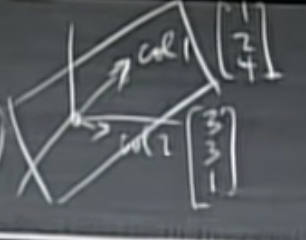
Column space (열공간) : all their combinations form a subspace called column space
벡터공간의 조합은 열 공간이라는 부분 공간을 형성한다.
즉, A 행렬은 R^2에 해당하며, 각각의 열은 하나의 열공간을 형선한다.
따라서, 두 벡터가 향하는 방향이 2개가 있고, 하나의 plane이 형성된다.
#MIT #Linear #algebra #lecture5 #Transposes #permutations #vectorspaces
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture9 Independence, Basis and Dimension (1) | 2024.12.10 |
|---|---|
| Lecture6 Column Space and Nullspace (2) | 2024.11.30 |
| Lecture #4 Factorization into A = LU (0) | 2024.11.24 |
| Lecture#3 Multiplication and Inverse Matrices (0) | 2024.11.23 |
| Lecture #2. Elimination with Matrices (1) | 2024.11.22 |