안녕하세요,
오늘은 9강 Independence, Basis and Dimension에 대해 학습하겠습니다.

- Linear independence : Vector가 있을 때, 모든 계수(coefficient)가 0인 경우를 제외하고, 선형 조합(Linear combination)으로도 0을 만들 수 없다면 이 벡터들은 독립(independent)하다고 한다.

A combination of the columns is zero, so the columns of this A are dependent.
열의 A 조합이 0이라면, A의 열은 종속(depdendent)이 된다.

We say vectors x1,x2,...xn are linearly independent (or just independent) if c1x1 +c2x2 +···+cnxn = 0 only whenc1,c2,...,cn areall0. When those vectors are the columns of A, the only solution to Ax = 0 is x = 0.
Two vectors are independent if they do not lie on the same line. Three vectors are independent if they do not lie in the same plane. Thinking of Ax as a linear combination of the column vectors of A, we see that the column vectors of A are independent exactly when the nullspace of A contains only the zero vector.
c1,c2,...,cn이 모두 0일 때에만 c1x1 +c2x2 +···+cnxn = 0이면 벡터 x1,x2,...xn은 선형으로 독립적(또는 그냥 독립적)이라고 한다. 이 벡터들이 A의 열일 때, Ax = 0의 유일한 해는 x = 0 이다.
두 벡터가 같은 직선 위에 놓여 있지 않으면 독립적이라고 한다. 세 벡터는 같은 평면 위에 놓여 있지 않으면 독립적이다. Ax를 A의 열벡터들의 선형결합으로 생각하면, A의 열벡터가 zero vector만을 포함할 때 A의 zero vector들은 정확히 독립적임을 알 수 있다.

If the columns of A are independent then all columns are pivot columns, the rank of A is n, and there are no free variables. If the columns of A are dependent then the rank of A is less than n and there are free variables.
A의 열이 독립적이면 모든 열은 피벗 열이고 A의 순위는 n이며 자유 변수가 없다. A의 열이 종속적이면 A의 순위는 n보다 작고 free Variables 한다.
정리
1. 어떤 행렬 A의 column vector가 선형 독립(Linear independence)이기 위해선 A에 대한 Null space가 오직 모든 변수가 0인 경우에 대해서만 존재해야 한다 (x1=0, x2=0,... xn=0).
2. 어떤 행렬 A에 대해서 Ax=0식에 대한 Null space가 x1=0, x2=0,... xn=0와 같이 모든 x가 0일 때를 제외한 다른 경우가 존재한다면, 그 행렬 A의 column vector는 종속(dependent)이다.
벡터들이 종속/독립인지 판별하는 방법
1. 독립(Independence)일때
- 벡터들을 행렬 A의 column으로 넣고 행렬 A의 Null space를 체크.
- 만약 이 행렬 A의 Null space(Ax=0)가 오직 zero vector만 존재할 경우, 이 벡터(행렬)들은 독립.
- 이때의 행렬 A의 Rank는 column의 수 n과 같다. (Rank=n)
- 따라서 free variable이 존재하지 않음
2. 종속(Dependence)일때
- 벡터들을 행렬 A의 column으로 넣고 행렬 A의 Null space를 체크.
- 만약 이 행렬 A의 Null space(Ax=0)가 zero vector이외의 다른 값이 존재할 경우, 이 벡터(행렬)들은 종속.
- 이때의 행렬 A의 Rank는 column의 수 n보다 작다. (Rank<n)
- 따라서 free variable이 존재한다.
- Spanning a space : 선형대수에서 span은 span a space라고 하며, 벡터들로 형성할 수 있는 공간을 말한다.

Vectors v1, v2, ...vk span a space when the space consists of all combinations of those vectors. For example, the column vectors of A span the column space of A.
If vectors v1, v2, ...vk span a space S, then S is the smallest space containing those vectors.
벡터 v1, v2, ...vk는 공간이 그 벡터들의 모든 조합들로 구성될 때 공간을 span한다. 예를 들어, A의 열 벡터들은 A의 열 공간을 span한다. 만약 벡터 v1, v2, ...vk가 공간 S를 span한다면, S는 그 벡터들을 포함하는 가장 작은 공간이다.
- Basis and dimension
Basis(기저) : 임의의 벡터가 어떤 공간을 "span"하면서, 독립인 경우를 뜻한다.
Dimension(차원) : 차원으로 주어진 공간들에 대한 모든 basis들은 같은 수의 vector를 가진다. vector의 수가 바로 그 공간의 Dimension이다.

A basis for a vector space is a sequence of vectors v1, v2, ...vd with two properties:
• v1, v2, ...vd are independent
• v1, v2, ...vd span the vector space.
The basis of a space tells us everything we need to know about that space.
벡터 공간의 basis는 다음과 같은 두 가지 성질을 가진 벡터 v1, v2, ...vd sequence이다.
1. v1, v2, ...vd는 독립적이다.
2. v1, v2, ...vd는 벡터 공간에 걸쳐 있다.
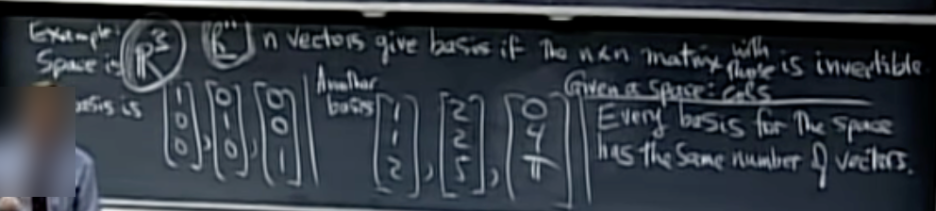
R3 3차원 공간을 예로 들어 설명하면, 독립이면서 3차원 공간 R3을 span하는 벡터는 단위행렬(Identity Matrix)를 생각할 수 있다.
Identity Matrix vector는 독립이며, vector에 상수를 곱하거나 더해도 Zero vector를 만들 수 없다. 왼쪽의 식은 Identity Matrix이 되며 Null space는 [0 0 0] T인 zero vector 한개만 해당한다.
하지만, 오른쪽의 Another basis도 있다.
[112]는 독립관계이지만 Basis는 아니고, [112] [225] [049] 세개의 차원 column vector는 독립관계이고 Basis 이다.
- Bases of a column space and nullspace
아래 식의 column vector들은 column space를 span하지만, independent하지 않는다.(사유 : col4 = col1, col3 = col1+col2).
따라서, A의 Column vector는 A의 column space C(A)의 Basis가 아니다.
A의 Column space C(A)의 Basis는 pivot column인 col1 과 col2이다. independent하면서 span한다.
결론적으로 행렬 A의 column space의 Basis는 pivot column인 col1과 col2 두개의 column vector이며, pivot column의 개수는 A의 Rank이다. > Rank(A=2)는 column space C(A)의 Dimension과 같다.
다음으로는 오른쪽의 N(A)를 확인해보면 각각의 special solution을 계산하면 0이 나오며, Vector의 선형 조합으로 Null space를 만들 수 있으므로 Basis이다.
따라서, 전체 Column 수(n) - Pivot variable(r)을 빼면 A의 Null space의 차원인 2가 된다.
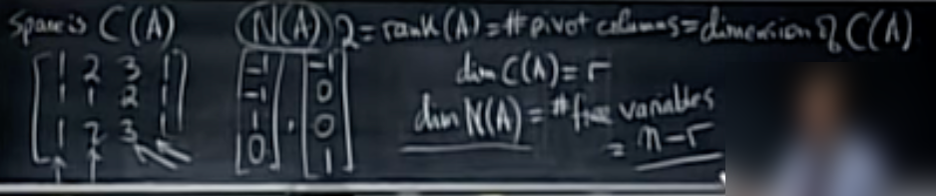
어떤 행렬 A의 rank는 행렬 A의 column space C(A)의 dimension(차원)이다.
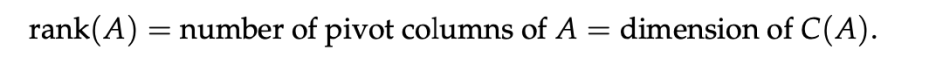
사진 설명을 입력하세요.
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture11 Matrix Spaces; Rank 1; Small World Graphs (0) | 2024.12.12 |
|---|---|
| Lecture10 The Four Fundamental Subspaces (1) | 2024.12.11 |
| Lecture6 Column Space and Nullspace (0) | 2024.11.30 |
| Lecture5 Transposes, Permutations, Vector Spaces (2) | 2024.11.26 |
| Lecture #4 Factorization into A = LU (0) | 2024.11.24 |