안녕하세요
오늘은Lecture11 Matrix Spaces; Rank 1; Small World Graphs 에 대해 학습하겠습니다.

Matrix spaces (New vector spaces)
New vector spaces = Matrix spaces, M = all 3 by 3 matrices
새로운 벡터공간은 행렬 공간이며, M은 모든 3 * 3 행렬이다.
또한, 행렬 M은 3가지 부분 공간인 Symmetric Matrix, Upper triangular Matrix, Diagonal Matrix를 가지고 있다.

Dimension & Basis
The dimension of M is 9; we must choose 9 numbers to specify an element of M. The space M is very similar to R9. A good choice of basis is:
차원(Dimension)은 행렬을 구성하고 있는 원소의 개수이므로 3*3행렬인 M의 차원은 9이다.
또한, 기저(Basis)도 9개이다.

Symmetric matrices (대칭행렬) : 주대각 원소들을 중심으로 대칭되는 지점의 원소들이 서로 같은 행렬
The subspace of symmetric matrices S has dimension 6.
대칭행렬 S의 부분공간은 차원 6을 갖는다. 차원이 6이기에 기저(Basis)도 6이다.

Upper triangular matrix (상삼각행렬) : 주대각 원소들을 중심으로 위로만 원소들이 존재하는 행렬
The dimension of U is again 6
Upper triangular matrix의 차원(dimension) 또한 6이며, 기저(Basis)도 6이다.
Diagonal matrix (대각행렬) : 대각 행에만 원소가 존재하고 나머지는 모두 0인 정방행렬
The subspace D = S ∩ U of diagonal 3 by 3 matrices has dimension 3.
대각행렬 D는 S(대칭행렬)과 U(상삼각행렬)의 교집합으로 차원(dimensnion)은 3이다. (그러므로 기저도 3)
S + U = M (but, 대칭행렬과 상삼각행렬의 합집합은? NO)
Is S ∪ U, the set of 3 by 3 matrices which are either symmetric or upper triangular, a subspace of M? No. This is a subspace of M. In fact, S + U = M.
대칭행렬과 상삼각행렬의 집합 S ∪ U는 M의 부분공간이 아니다. 다만, 두개를 합한다면 부분공간이 된다.
M의 차원(Dimension)은 9이며, 기저(Basis)도 9이다.

Differential equations(미분방정식)
Another example of a vector space that’s not Rn appears in differential equa tions.
R^n 즉, Vector를 가지지 않는 또 다른 예는 미분방정식이다.

위의 해들은 미분방정식의 null space로, comple solution(완전해)를 정의하면 아래와 같다.

This solution space is a two dimensional vector space with basis vectors cos x and sin x. (Even though these don’t “look like” vectors, we can build a vector space from them because they can be added and multiplied by a constant.)
이 solution space(해 공간)은 vector cos x와 sin x를 갖는 2차원 벡터공간이다. (선형 결합으로 표현할 수 있기 때문)
*방정식의 해 공간에 대한 기저를 찾는 것 = 선형미분방정식을 푸는 것 ( Basis들을 vector라 부르는 것은 선형 결합이 가능하기 때문이다.)

Rank one matricies
아래의 A의 1행과 2행은 종속이며, 열도 동일하게 종속이다.
Every rank 1 matrix A can be written A = UVT, where U and V are column vectors. We’ll use rank 1 matrices as building blocks for more complex matrices.
모든 rank1 matrix A는 A = UV^T로 표기할 수 있고, U와 V는 열 벡터이다. 쉽게 말하면, Column과 row vector를 순서대로 곱하면 rank1의 행렬이 만들어진다.
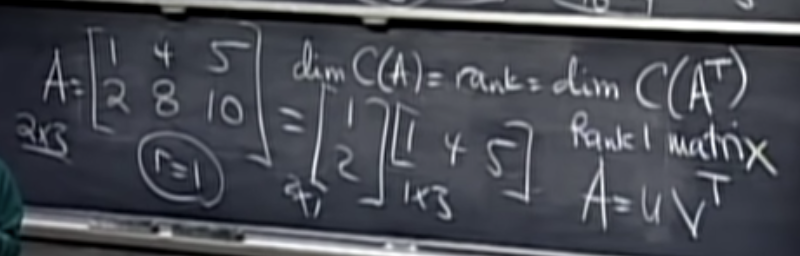
Rank 4 matrices
A has rank 1, the dimension of this nullspace is n − r = 3. The left nullspace contains only the zero vector, has dimension zero, and its basis is the empty set. The row space of A also has dimension 1.
A는 rank1을 가지며, nullspace의 차원은 n - r = 3이다. 왼쪽 nullspace는 zero vector만을 포함하고, 차원은 0을 가지며, 기저(basis)는 빈 집합입니다. A의 행 공간(row space)도 차원 1을 가진다.
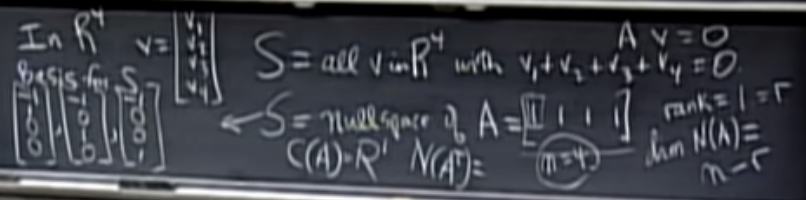
Small world graphs
노드사이의 거리에 대한 행렬을 그래프로 표현하였다.
정리
1. Matrix spaces (New vector spaces)는 Symmetric Matrix, Upper triangular Matrix, Diagonal Matrix를 가지고 있다.
1) Symmetric matrices (대칭행렬) : 주대각 원소들을 중심으로 대칭되는 지점의 원소들이 서로 같은 행렬
2) Upper triangular matrix (상삼각행렬) : 주대각 원소들을 중심으로 위로만 원소들이 존재하는 행렬
3) Diagonal matrix (대각행렬) : 대각 행에만 원소가 존재하고 나머지는 모두 0인 정방행렬
기타) S + U = M (but, 대칭행렬과 상삼각행렬의 합집합은? NO)
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture14 Orthogonal Vectors and Subspaces (0) | 2024.12.17 |
|---|---|
| Lecture12 Graphs, Networks, Incidence Matrices (0) | 2024.12.14 |
| Lecture10 The Four Fundamental Subspaces (1) | 2024.12.11 |
| Lecture9 Independence, Basis and Dimension (0) | 2024.12.10 |
| Lecture6 Column Space and Nullspace (0) | 2024.11.30 |