MIT GilbertStrang 교수님의 Linearalgebra 14강 Orthogonal Vectors and subspaces

The “big picture” of this course is that the row space of a matrix’ is orthogonal to its nullspace, and its column space is orthogonal to its left nullspace.
Row space & nullspace는 orthogonal(직교)한다. Column space & left nullspace도 orthogonal(직교)한다.
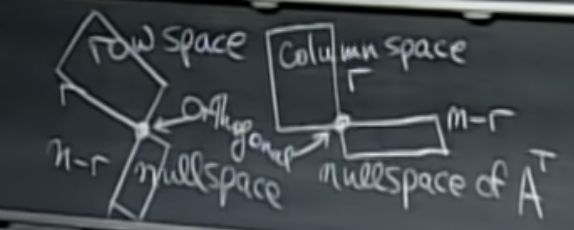
Orthogonal vectors (직교 벡터)
Orthogonal is just another word for perpendicular. Two vectors are orthogonal if the angle between them is 90 degrees.
직교는 다른 말로 수직(Perpendicular)이다. 두 벡터들이 90도로 수직을 이룰 때 직교한다고 할 수 있으며, right triangle (직각 삼각형)을 이룬다.
we can use the Pythagorean theorem to prove that the dot product xT y = yT x is zero exactly when x and y are orthogonal.
피타고라스 정리(Pythagorean theorem)에 의해 ||x||2 + |y||2 = |x+y||2이다. 또한 xT y = yT x 는 0이다.
중요한 것은 모든 벡터는 zero vector와 직교(Orthogonal)한다.
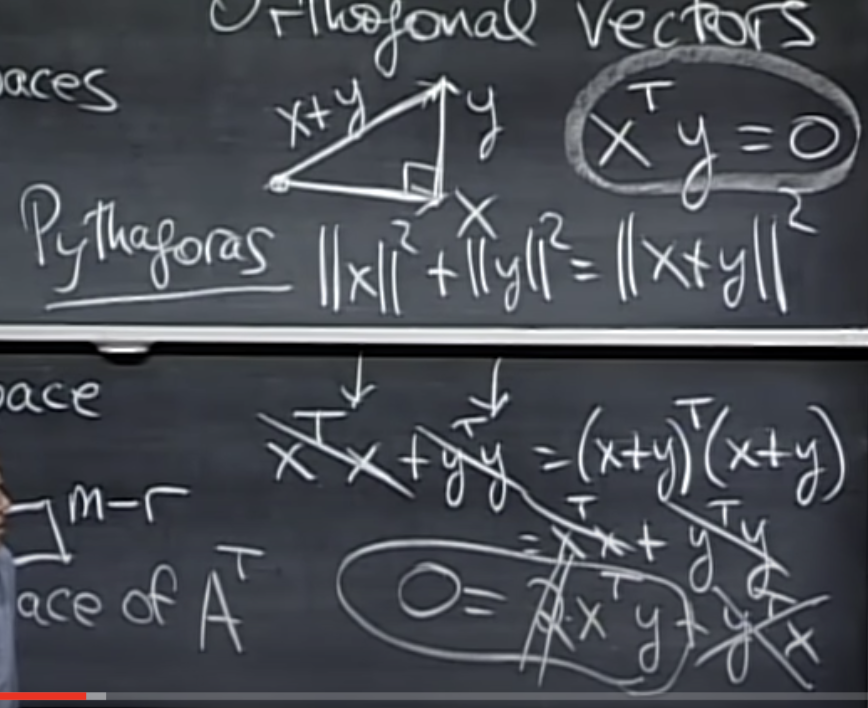
Orthogonal subspaces (부분 공간의 직교)
Subspace S is orthogonal to subspace T means: every vector in S is orthogonal to every vector in T.
부분공간 S가 부분공간 T에 직교한다는 말은, S의 모든 벡터가 T에 있는 모든 벡터와 직교한다는 것이다.

Nullspace is perpendicular to row space (row space is Orthgonal to nullspace)
The row space of a matrix is orthogonal to the nullspace, because Ax = 0 means the dot product of x with each row of A is 0. But then the product of x with any combination of rows of A must be 0.
Ax=0은 각 행이 0인 x의 점(dot) 곱을 의미하기 때문에 행렬의 행(row) 공간은 nullspace와 직교한다.
하지만, A의 행 조합아 있는 x의 곱은 반드시 0이다.
Dimension of row space은 rank인 r차원이고, Dimension of Nullspace는 n-r차원이다.
따라서, 두 공간이 직교한다는 것은 Rn 차원의 공간을 두 개의 수직한 부분 공간으로 나눈 것이다.
아래의 내용을 참고하면 n=3, r=1 이므로 dimN(A) = 2


The nullspace and the row space are orthogonal complements in Rn. The nullspace contains all the vectors that are perpendicular to the row space, and vice versa.
Nullspace & row space는 Rn에서 직교 여집합이다. Nullspace는 row space에 수직인 모든 vector를 포함하며 그 반대도 동일하다.

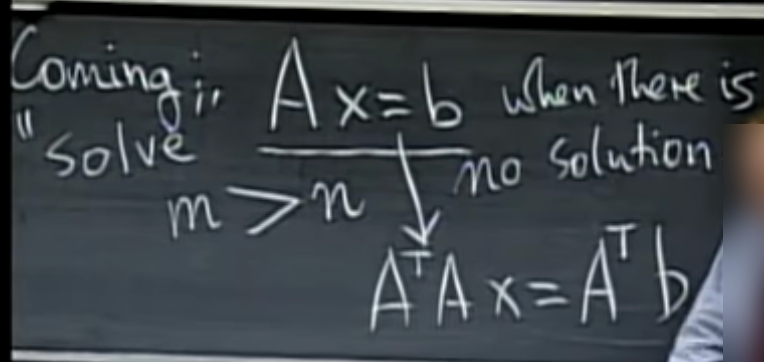
We conclude that AT A is invertible exactly when A has independent columns.
A가 독립적인 열을 가질 때, AT A는 invertible이라고 한다.

정리
1.Orthogonal vectors (직교 벡터) : 두 벡터들이 90도로 수직을 이룰 때 직교한다고 할 수 있으며, right triangle (직각 삼각형)을 이룬다. *모든 벡터는 zero vector와 직교(Orthogonal)한다.
2.Orthogonal subspaces (부분 공간의 직교) : 부분공간 S가 부분공간 T에 직교한다는 말은, S의 모든 벡터가 T에 있는 모든 벡터와 직교한다는 것이다.
3. null space와 row space는 R^n 차원에서 서로 직교하는 complements다.
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture16 Projection Matrices and Least Squares (1) | 2024.12.24 |
|---|---|
| Lecture15 Projections onto Subspaces (2) | 2024.12.19 |
| Lecture12 Graphs, Networks, Incidence Matrices (0) | 2024.12.14 |
| Lecture11 Matrix Spaces; Rank 1; Small World Graphs (2) | 2024.12.12 |
| Lecture10 The Four Fundamental Subspaces (1) | 2024.12.11 |