안녕하세요,
"비전공자의 인공지능 고군분투기" First man입니다.
오늘은 제가 석사과정을 밟기 위해 공부하였던 선형대수학에 대해 작성하고자 합니다.
대학원 컨텍 시에, UNIST 교수님께서 들으라고 말씀하셨던
Gilbert Stang 교수님의 MIT Linear Algebra 강의는 많은 인공지능 학석사 분들이 기초를 다지거나
다시 한 번 선형대수학을 공부할 때 굉장히 유용한 강의로 평가받고 있습니다.
따라서 석사과정을 밟고 있는 저도 매주 수업시간에 해당 강의로 퀴즈를 보고 있습니다.
교수님께서 말씀하시길 "선형대수학은 시간이 지나면 잊혀지기 때문에 3~4번은 지속적으로 공부를 해줘야 한다." 라고 말씀하신 만큼
인공지능 석사 진학을 희망하시는 분,
비전공인데 어디서 부터 시작해야 할 지 막막하신 분,
기타 인공지능에 대해 공부하고 싶으신 분
위의 3가지에 해당되시는 분들은 해당 강의를 꼭 들으시고,
시간이 안되시는 분들은 제가 하는 리뷰를 통해 도움이 되셨으면 좋겠습니다.
그럼 지금부터 리뷰를 시작하겠습니다.
The Geometry of Linear Equations
The fundamental problem of linear algebra is to solve n linear equations in n unknowns
A case when we have some number of equations, say n equations and n unknowns.
So an equal number of equations and unknowns.
Ex) Two equations, two unknowns.

What is the coefficient matrix? A
A matrix is just a rectangular array of numbers.
Two rows and two columns .
A : the matrix of coefficients
X : vector of unknowns
b : right-hand side is also a vector
> linear equations are A x equal b.
행(Row) Picture

Plot the points that satisfy each equation. The intersection of the plots (if they do intersect) represents the solution to the system of equations.
Looking at Figure 1 we see that the solution to this system of equations is x = 1, y = 2.
쉽게 설명하자면, 선형 방정식들의 그래프를 각각 그린 후 서로 만나는 교점이 선형 시스템의 해가 된다.

열(Column) Picture
In the column picture we rewrite the system of linear equations as a single equation by turning the coefficients in the columns of the system into vectors:
쉽게 설명하자면, 위의 행과 다르게 열의 관점으로 선형 시스템을 보는 것이다.
열 벡터들의 선형 결합으로 표현이 가능하다.
Given two vectors c and d and scalars x and y, the sum xc + yd is called a linear combination of c and d. Linear combinations are important throughout this course.
As we see from Figure 2, x = 1 and y = 2, agreeing with the row picture in Figure 2.

Figure 2

파란색 Column1
빨간색 Column2
빨간색 점선 2 Column2
초록색 Column3
행(Row) 과 열(Column) Picture
세번 째는, Row와 Column picture로 문제를 푸는 것이다.
Row picture로 선형방정식 좌표계를 그리면 오른쪽과 같이 평면이 겹치는 영역이 나타난다.
행렬은 Linear independence 이므로, 겹치는 평면을 구할 수 있다.

The main point is that the three planes, because they are not parallel, they are not special.
The row picture consists of three planes and, if everything works right, three planes meet in one point and that is a solution.
Using column picture,

One of those is obviously the right one.
Column three is actually the same as b in this particular problem.
If the score of b change like under picture [1, 1, -3]

x =1, y =1 and z = 0
Linear Independence
Q: Can I solve Ax = b for every b?
(Do the linear combs of the colomns fill 3-D space?)
A: Yes
If the answer is “no”, we say that A is a singular matrix. In this singular case its column vectors are linearly dependent; all linear combinations of those vectors lie on a point or line (in two dimensions) or on a point, line or plane (in three dimensions). The combinations don’t fill the whole space.
Matrix Picture
How do we multiply a matrix A by a vector x?

One method is to think of the entries of x as the coefficients of a linear combination of the column vectors of the matrix:
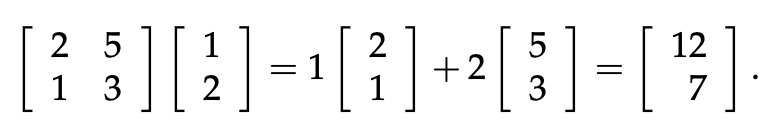


Ax is a combination of columns of A.
이상으로 MIT Gilbert Strang 교수님의 Linear Algebra 1강 리뷰를 마치도록 하겠습니다.
다음에는 다음 강의로 인사드리겠습니다.
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture5 Transposes, Permutations, Vector Spaces (2) | 2024.11.26 |
|---|---|
| Lecture #4 Factorization into A = LU (0) | 2024.11.24 |
| Lecture#3 Multiplication and Inverse Matrices (0) | 2024.11.23 |
| Lecture #2. Elimination with Matrices (1) | 2024.11.22 |
| An Overview of Linear Algebra (1) | 2024.11.21 |