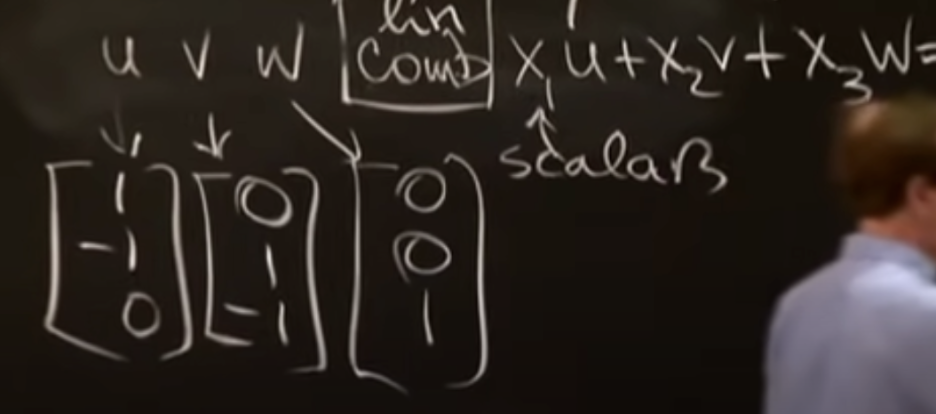비전공자의 인공지능 고군분투기

MIT Gilbert Strang교수님의 Linear Algebra 18강 Properties of Determinants 리뷰입니다. DeterminantsThe determinant is a number associated with any square matrix; det A or |A|determinant는 any square matrix와 연관되어 있는 숫자로써, det A 혹은 |A|로 표기한다.The matrix is invertible exactly when the determinant is non-zero.행렬은 행렬식이 0이 아닐 때 invertible하다.  Properties모든 크기의 정방행렬의 행렬식에 대한 공식을 줄 것이다.특징으로는 아래와 같다. 1. det I = 1 2. 행..

안녕하세요,오늘은 MIT Gilbert Strang 교수님의 선형대수학 Lecture12 Graphs, Networks, Incidence Matrices에 대해 학습하겠습니다. Graph : Nodes, Edge그래프는 꼭짓점인 Node와 변인 Edge로 구성되어 있다.아래의 그래프는 꼭짓점 4개 (N=4), 변 5개(M=5)로 이루어져 있다.Incidence Matrix (근접행렬)The incidence matrix of this directed graph has one column for each node of the graph and one row for each edge of the graph꼭짓점인 Node의 개수를 column으로, 변인 Edge의 개수를 row로 만들어 5*4 근접행렬을 ..

안녕하세요,오늘은 9강 Independence, Basis and Dimension에 대해 학습하겠습니다. Linear independence : Vector가 있을 때, 모든 계수(coefficient)가 0인 경우를 제외하고, 선형 조합(Linear combination)으로도 0을 만들 수 없다면 이 벡터들은 독립(independent)하다고 한다.A combination of the columns is zero, so the columns of this A are dependent.열의 A 조합이 0이라면, A의 열은 종속(depdendent)이 된다.We say vectors x1,x2,...xn are linearly independent (or just independent) if c1x1 ..

안녕하세요,오늘은 MIT Gilbert Strang교수님의 Linear algebra 6강 Column Space and Nullspace에 대해 리뷰해보도록 하겠습니다.   Vector SpaceA vector space is a collection of vectors which is closed under linear combinations. In other words, for any two vectors v and w in the space and any two real numbers c and d, the vector cv + dw is also in the vector space. A subspace is a vector space contained inside a vector space. Ve..

안녕하세요, 오늘은 MIT 선형대수(Linear algebra) 5강 Transposes, permutations, vector spaces에 대해 학습해보겠습니다.   Permutations(치환)Multiplication by a permutation matrix치환행렬은 행교환 (row exchange)을 수행하는 행렬이다. 행교환은 pivot이 0인 경우에 반드시 필요하다. P swaps the rows of a matrix; when applying the method of elimination we use permutation matrices to move ze­ros out of pivot positions. Our factorization A = LU then becomes PA = LU,..

안녕하세요, 오늘은 MT Gilbert Strang 교수님의 Linear Algebra 수업 Lecture4, Factorization into A = LU 에 대해 다루어보겠습니다.      Inverse of a productThe inverse of a matrix product AB is B−1 A−1. AB의 역행렬은 B−1 A−1이다.  Transpose of a product행과 열을 바꿀 때 사용the entry in row i column j of A is the entry in row j column i of A^T열I와 행J의 A를 열J와 행I으로 바꾼 것을 A^T라고 한다. The transpose of a matrix product AB is BTAT. For any invert..

안녕하세요, 오늘은 MIT Gilbert Strang교수님의 선형대수 강의 Lecture#2 Elimination with Matrices로 공부해보도록 하겠습니다.  Method of EliminationElimination is the technique most commonly used by computer software to solve systems of linear equations. It finds a solution x to Ax = b whenever the matrix A is invertible. In the example used in class,The number 1 in the upper left corner of A is called the first pivot.The first..

안녕하세요, 인공지능 전공자라면 정말 중요하지만 어렵게 느끼는 선형대수학 입니다. 오늘은 MIT GilbertStrang 교수님의 2강인 An Overview of Linear Algebra 에 대해 리뷰해보겠습니다.   This is an overview of linear algebra given at the start of a course on the math­ ematics of engineering.  VectorsWhat do we do with vectors? Take combinationsWe can multiply vectors by scalars(such as under x1,x2,x3), add, and subtract. Given vectors u, vand w we can form ..