MIT Gilbertsrang 교수님의 Linear algebra 17강 Orthogonal Matrices and Gram-Schmidt 배우겠습니다.

Orthonormal Vectors (직교벡터) : 길이가 1인 모든 열벡터가 서로 직교하는 것
All have (normal) length 1 and are perpendicular (ortho) to each other. Orthonormal vectors are always independent.
모두 (정규) 길이가 1이고 서로 수직이다. 직교 벡터는 항상 독립적이다. 나아가, Orthonormal vector = orthogonal and unit vector 이다. 즉 every q is orthogonal to every other q.이다.

Orthonormal matrix (직교 행렬)
QTQ=I (Q columns = orthonormal)
Matrices with orthonormal columns are a new class of important matrices to add to those on our list: triangular, diagonal, permutation, symmetric, reduced row echelon, and projection matrices.
Orthonormal columns을 갖는 행렬은 triangular, diagonal, permutation, symmetric, reduced row echelon, and projection matrices list에 추가할 새로운 종류의 중요한 행렬 이다.

아래는 Square orthogonal matrix와 Rectangular orthogonal matrix 설명하였다.
첫번째로, Square orthogonal matrix (핵심은 If Q is square, then QTQ = I tells us that QT = Q−1. )
We’ll call them “orthonormal matrices”. A square orthonormal matrix Q is called an orthogonal matrix. If Q is square, then QTQ = I tells us that QT = Q−1.
Square orthonormal matrix Q를 orthogonal matrix라고 한다.Q가 제곱이면 QTQ = I 는 QT = Q−1.
두번째로, Rectangular orthogonal matrix( square root로 나눠주지 않아서 nice하다.)
각각의 column이 orthonormal 하므로, orthonormal basis하다고 할 수 있다.


Orthonormal columns are good
Suppose Q has orthonormal columns. The matrix that projects onto the column space of Q is: P = QT(QTQ)−1QT.
Q는 정상 열을 가지고 있다고 가정하면,Q의 열 공간에는 다음과 같다 : P = QT(QTQ)−1QT.
If the columns of Q are orthonormal, then QTQ = I and P = QQT. If Q is square, then P = I because the columns of Q span the entire space.
Q의 열이 orthonormal이면, QTQ = I and P = QQT이다. Q가 square면, Q의 열이 전체 공간에 걸쳐 있으므로 P = I 입니다.

즉, Q를 이용한다면 inverse를 계산하지 않아도 된다.

Gram-Schmidt
With elimination, our goal was “make the matrix triangular”. Now our goal is “make the matrix orthonormal”.
Elimination에서의 목표는 triangular matrix를 만드는 것이었다. 지금은 orthonormal matrix를 만드는 것이다.
We start with two independent vectors a and b and want to find orthonormal vectors q1 and q2 that span the same plane. We start by finding orthogonal vectors A and B that span the same space as a and b.
두 개의 독립적인 벡터 a와 b로부터 시작하고, 같은 평면에 걸쳐 있는 직교벡터 q1과 q2를 찾는다. a와 b와 같은 공간에 걸쳐 있는 직교벡터 A와 B를 찾는 것으로 시작한다.
Let A = a. We get a vector orthogonal to A in the space spanned by a and b by projecting b onto a and letting B = b − p. (B is what we previously called e.)
A = a라고 하고, b를 a에 사영하고 B = b - p를 허용함으로써 a와 b에 걸쳐 있는 공간에서 A와 직교하는 벡터를 얻는다. (B는 우리가 이전에 e라고 불렀던 것이다.)
If we multiply both sides of this equation by AT, we see that ATB = 0.
What if we had started with three independent vectors, a, b and c?
Then we’d find a vector C orthogonal to both A and B by subtracting from c its components in the A and B directions :
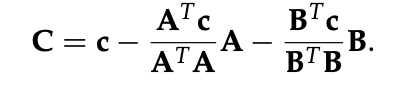
이 방정식의 양변에 AT를 곱하면, ATB = 0.
만약 a, b, c 세 개의 독립적인 벡터로 시작했다면 ? 그러면 A와 B 방향의 c 성분을 빼면 A와 B 모두에 직교하는 벡터 C를 찾을 수 있다

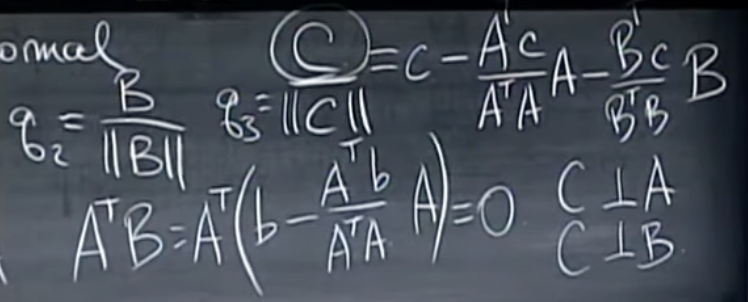
When we studied elimination, we wrote the process in terms of matrices and found A = LU. A similar equation A = QR relates our starting matrix A to the result Q of the Gram-Schmidt process. Where L was lower triangular, R is upper triangular.
elimination은 A=LU를 주고, Gram-Schimidt 과정을 matrix 형태로 보면 A=QR이라는 결과가 나온다.
그리고 L은 lower triangular, R은 upper triangular
Notice that R = QT A. This makes sense; QT Q = I.
R = QT A. 말이 된다; QT Q = I.
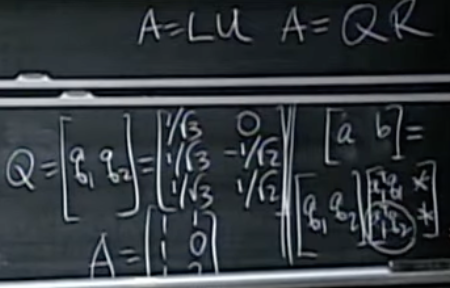
정리
Square orthogonal matrix (핵심은 If Q is square, then QTQ = I tells us that QT = Q−1. )
두번째로, Rectangular orthogonal matrix( square root로 나눠주지 않아서 nice하다.)
Gram-Schmidt : columns들을 columns orthonormal하게 하는 것.(*columns들은 independent)
Gram-Schmidt matrix : A=QR
#MIT #Gilbertstrang #Linearalgebra #17강 #Orthogonalmatrices #Gram-Schmidt
'7. 수학공부 > 선형대수학' 카테고리의 다른 글
| Lecture18 Properties of Determinants (1) | 2024.12.26 |
|---|---|
| Lecture16 Projection Matrices and Least Squares (0) | 2024.12.24 |
| Lecture15 Projections onto Subspaces (0) | 2024.12.19 |
| Lecture14 Orthogonal Vectors and Subspaces (0) | 2024.12.17 |
| Lecture12 Graphs, Networks, Incidence Matrices (0) | 2024.12.14 |