CS231n 3강 공부 및 리뷰를 시작하겠습니다. 인공지능을 준비하시는 분들에게도 도움이 되었으면 좋겠습니다.
지난 2강 복습
컴퓨터가 비전을 인식하는데 여러 challenge들이 있다. (각도, 조명, 변형, 은폐/은닉, 배경, 클래스 내의 variatione들) 그럼에도 기계는 사람의 능력을 넘어서는 classify를 할 수 있게 되었다.
Data driven approach - 1) nearest neighbor 2) Linear classifier(매칭 탬플릿, 클래스 기반 구분)
오늘은 Score에 대해 불만족하는 정도를 정량화하는 Loss Function 정리 및 Loss function을 최소화하는 parameter 값들을 찾는 과정인 Optimization을 배워보도록 한다.
1. Loss function 정리 2가지 방법 (SVM과 Softmax)
2. Optimization


3개의 학습용 이미지와 3개의 class로 구성되어 있다.
f(x, W) = Wx 함수를 이용했을 때의 결과 값을 볼 수 있다.
여기서 2가지 Loss에 알아보겠다.
1. Loss Function
1) SVM- Hinge loss

xi : 이미지, yi : label, score vector : s = f(xi, W)
SVM loss는 파란색 칸으로 나타낸다.
max 함수는 0과 오른쪽 항중에 더 큰쪽을 취하겠다는 의미
sj : 잘못된 label의 score, syi : 제대로된 label의 score, 1 : safety margin
해석하는 방식
1) sj - (syi-1) 이렇게 된다. correct label의 score - 1 보다 큰 incorrect label이 있다면 Loss는 0보다 크게 된다. 그리고 correct label의 score가 다른 incorrect label score 보다 1 이상 크면 Loss는 0이 된다.
첫번째 고양이 이미지에 대해서 correct score 3.2 / 개구리 -1.7 (가운데 수치 제거)
나머지 2개도 동일하게 진행.

최종 로스값은 4.6
Q: what if the sum was instead over all classes?(including j=y_i)
A: j=y_i가 같은 경우까지 sum하면 모두 1씩 증가하기 때문에 평균 값인 최종 Loss값도 1만큼 증가하게 된다.
Q: what if we used a mean instead of a sum here?
A: 큰 의미는 없다.
Q: what if we used 아래

A: 상황이 달라진다 제곱을 해준다는건 non linear하게 되기 때문에 차이가 있다.
Q: what is the min/max possible loss?
A: 최저값은 0 (0과 다른 항을 비교해서 더 큰 값을 선택하는 것이기 때문에)
최대값은 무한대 (다른 항이 무한대가 될 수 있기 때문에)
Q: usually at initialization W are small numbers, so all ~= 0. What is the loss?
A: 2 (세개의 class가 각각 2가 나오게 되어서,,, 10개 class라면 1+1을 9번해서 9라는 값이 나옴.)
일반화를 하게 되면 class의 개수 -1 이라는 것을 초기의 loss 값을 가진다는 것을 알 수 있다. 최초에 학습을 시작할 때, Loss 값이 이 규칙에 맞는지 확인하면 학습의 시작이 제대로 되고 있는지를 파악할 수 있어서 유용하다. 이것을 sanity check이라 한다.

x: image column vector, y: label integer 값, W: parameter인 weights matrics
score를 w와 x의 단연산을 통해 구하고, margin을 svm loss 공식에 맞게 구하게 되면 margin y 은 0으로 처리(j와 yi가 같은 경우에는 0으로 처리해준다)
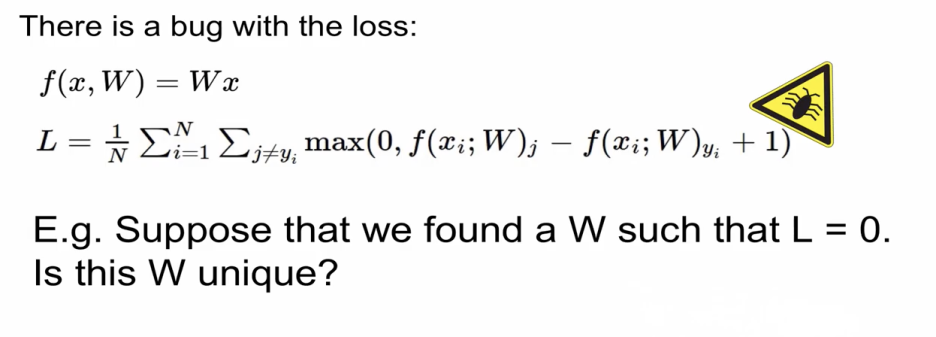
Loss 값에 버그가 있다.
Q: L를 0으로 만드는게 unique 한가?
A: no, 0이라는 loss 값은 만드는 weight가 unique하지 않다.

따라서, 우리는 Unique한 weight 값을 결정해주기 위해서 Regularization을 도입한다.
L2 regularization과 L1 regularization 그리고 Dropout 많이 쓰인다.

Regularization은 W가 얼마나 괜찮은지의 정도를 측정하는 역할

왼쪽 data loss는 : 학습용 데이터들을 최대한 최적화 하려고 노력하는 값

오른쪽 regularization loss는 test set 쪽에 최대한 일반화를 하려고 노력하는 것
* 따라서, data loss항과 regularization loss항이 서로 싸우면서 data에 가장 fit하고 가장 최적화된 작은 weight 값 추출.
a way of trading off training lass and generalization loss on test set
- Regularization이 들어가면 비록 train error는 커진다. (Train data에 대한 정확도는 안좋아지겠지만) 결과적으로 우리의 목적인 test set에 대한 performance는 좋아진다.
- Regularization 입장에서는 weight가 모두 0에 가깝기를 원한다.(loss 가 작아지니까) 하지만, data loss 입장에서는 weight가 0일 수는 없다.(classify를 해야하니까) 따라서, 양쪽이 서로 싸우면서 test set에 대해 좀 더 일반화된 훌륭한 결과를 낼 수 있다.


두개의 결과가 1로 같다. 그렇다면 regularization은 어떤 weight를 선호할까? W2를 더 선호한다.
기본적으로 W2가 X vector의 모든 원소들을 염두한다. W1은 첫번째만 염두(나머지는 0이니까)한다.
그래서 L2 regularization은 weight을 최대한 spread out해서 모든 Input 고려하기 원한다.(diffuse over everything)
즉 동일한 score라면 최대한 spread out되는 것을 선호한다.
2) Softmax - Cross entropy loss
(=Multinominal logistic Regression) 이항에 대한 logistic regression을 다차원으로 일반화 한 것

Scores 는 class를 normalized하지 않은 log화한 확률
제대로된 class에 대한 log의 확률을 최대화 하고자 하는 것.(정확한 class의 -log 확률을 최소화 하자는 것)

정교화 하지 않은 score를 확률로 나타내고자 exp 하고 , 정규화 하면 확률로 나온다. (전체 합이 1이 되는 확률)
Q: What is the min/max possible loss L_i
A: X축은 확률이기 때문에 (확률은 1보다 클 수 없으니 0과 1사이에 머문다.)
최소값은 0, 최대값은 무한대(=SVM 과 같다.)
잘 맞추면 확률이 1에 가까워지니 loss는 0에 가까워지는 것이고
반대로 아주 못맞추면 확률이 0으로 나타나고 Loss가 무한대로 나타난다.
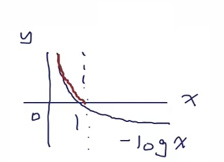
Q: usually at initialization W are small numbers, so all s~= 0.What is the loss?
A: -log 1/ class의 개수 (따라서, sanity check 활용해서 학습하기 전에 수치가 나오는지 확인하고 진행하면 더 정교해진다.)
최초 score가 0들로 나오고 >exp 하면 각 1,1,1 이 되고 > 합이 1이되니까 1/3나누면 확률은 1/3이 된다.
즉 -log 1/3이 된다.
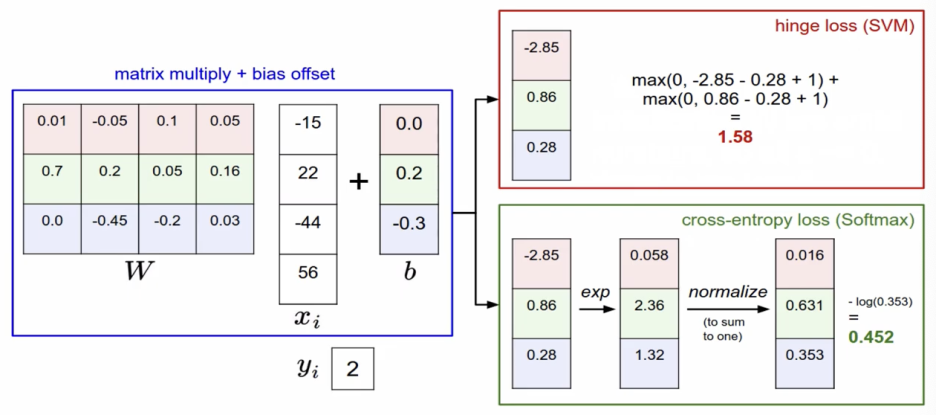
실제로는 Softmax가 더 많이 사용되기는 한다.

Q: Suppose I take a datapoint and I jiggle a bit. What happens to the loss in both cases?
A: SVM은 뒤 safety margin을 통해 흔들리지 않는 굳건함을 제공해준다.따라서, Loss값 불변
Softmax는 모든 인자들을 고려하기에 변한다.
정리하자면, SVM은 값들의 변화에 둔감하다. (민감하지 않다.)
Softmax는 값들의 변화에 민감하다.

2. Optimization
(=Loss를 minimize 하는 weight를 찾아가는 과정)
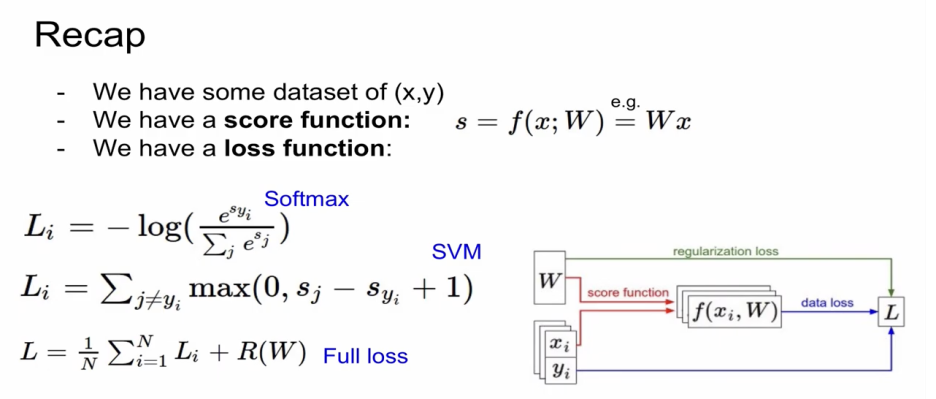
regularization loss의 경우에는 데이터와 상관이 없다. 즉, weight만의 함수다. (weight에만 영향을 받는다.)
Optimization(최적화)하는 몇가지 전략이 있다.
Strategy #1. Random search를 하지 않는다.
산 속에서 여기 저기 최적 경로를 찾아가는 것이기 때문에 말이 안되는 전략

1,000번을 돌리는데 다 random하게 선택한다.

최종적인 예측 정확도는 15.5% (State of the art가 95%)
Strategy #2. Follow the slope
경사를 따라 내려가는 전략

1차원의 경우에는 함수를 미분하는 것 (수치적으로 경사를 구함)
다차원의 경우에는 vector의 형태로 나타난다.
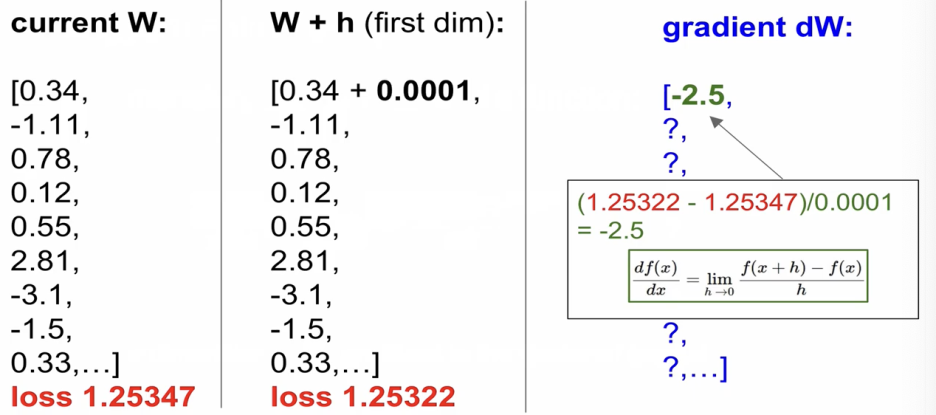
gradient가 음수라는 것은 내려가는 방향으로 기울기가 아래로 되어있다.

Loss 변화 없다는 건 gradient dw가 0이 되고, 기울기가 없다.

직접 계산해서 Gradient를 계산하는 것을 numerical gradient라고 하는 것인데
정확한 값이 아니라 근사치를 얻게 되는 것이고 평가가 매우 느리다.
단점 : 1) approximate, 2) very slow to evaluate
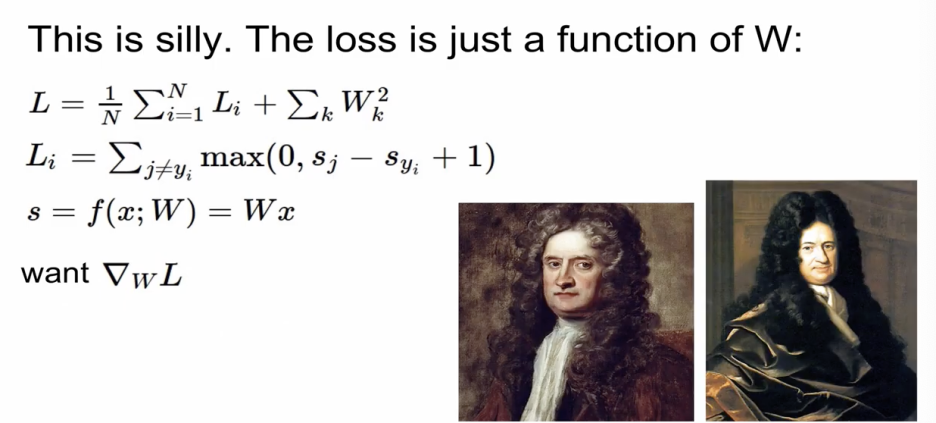
결정적으로 이렇게 하는 것은 어리석다.
loss는 기본적으로 weight의 function이기 때문에
우리가 구하고자 하는 것은 결국 weight가 변할 때, loss가 얼마만큼 변하냐 이기 때문에
미분만 알면 쉽게 구한다.
미분을 통해 Gradient를 구하는 방식 : analytic gradient
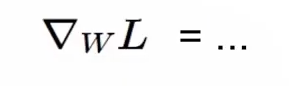

미분을 통해 구하면 쉽게 구한다.

정리하자면,
Numerical gradient는 근사치이고 느리지만, 코드로 작성하기 쉽다.
analytic gradient는 정확하고 빠르지만, 코드로 작성하면 에러가 날 가능성이 있다.
실제로는 analytic gradient만 사용한다. 다만, 계산이 정확히 되고 있는지 검토하고자 numerical gradient를 활용한다. 이러한 체크하는 것을 gradient check라고 한다.
1) Full-batch Gradient Descent

loss_function data weights을 전달해 줌으로서 gradient를 구하고,
구한 gradient와 step size를 곱해주어서 기존 weight에 빼줌으로서 parameter update를 한다.
*step_size = learning rate(알파)
gradient 값만큼 weights를 감소시켜야 하기에 step_size 앞에 - 부호가 생긴다.
*참고 learning rate인 alpha와, 앞의 regularization strength인 lambda 는 가장 골치 아플 수 있는 hyperparametor이다. 따라서, validation을 이용해서 최적의 값을 찾아줘야하는 것이 숙제이다.
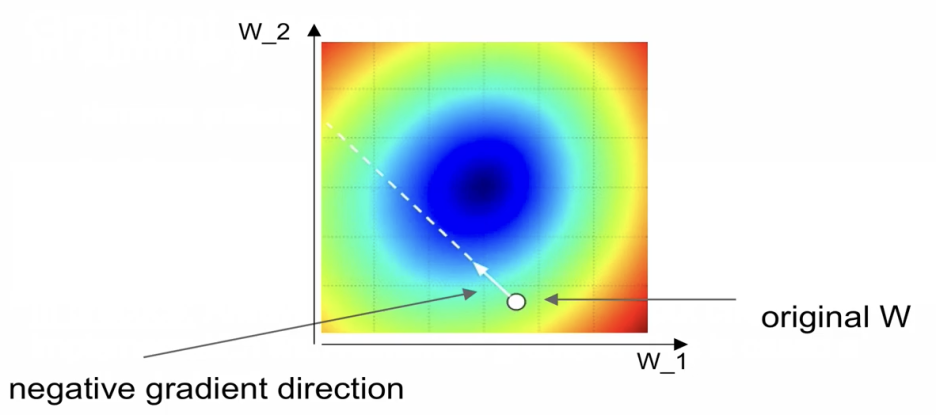
original W가 있을 때 음의 gradient direction으로 이동하면서 최적화를 해나가는게 gradient descent가 된다.
트레이닝 set 전체를 사용하는 Full-batch Gradient이었다면,
지금부터는 현실에 유용한 Mini-batch gradeint를 배우도록 한다.
2) Mini-batch Gradient Descent
training set중의 일부만을 활용해서 효율적이고, 성능을 높이는 역할을 하게 된다.

training set의 일부만으로 gradient 개선, 이를 통해 parameter 업데이트,
다음 mini-batch로 또다시 학습시켜서 gradient를 개선하고 또다시 parameter 업데이트 반복
일반적으로 mini batch size는 32/64/128/256 형태로 나타난다.
AlexNet은 256개를 활용
환경(CPU/GPU의 메모리 수준)에 적합한 수치를 설정해주면 된다.

Mini-batch를 사용함에 noise가 보이게 된다. 특정 128개의 data만 parameter를 업데이트 하는 방식이기에
경우에 따라 loss가 잠깐 증가하고 내려오는 것이 반복되나, 장기적으로 보았을 때에는 서서히 내려간다.

learning rate 설정에 따른 loss 값의 변화
Learning rate을 크게 잡으면 노란색처럼 Loss가 diverge/ explode
Learning rate가 너무 작으면 파란색처럼 slow convergence (오래걸림)
Learning rate가 높으면 초록색처럼 high learning rate( loss가 최저점으로 가지 못하는 현상, global minimum에 빠지지 않고 local minima에 빠지게 되는 경우)
잘 설정하면 빨간색처럼 빠른 시간에 loss가 최소화된다.
높게 설정했다가 점점 낮춰가는 decay 설정을 하게 된다.

momentum : loss가 줄어드는 속도까지 tracking하면서 진행하기 때문에 더 빠른 효과..
다양한 방법은 5강정도에서 다룰 예정

빨간색 SGD : 끝도없이 계속 가고 (느림)
초록색 Momentum : 아래까지 오버슈팅했다가 제 자리를 빠르게 찾아감
다음으로는 Image classification 파이프 라인이 어떻게 구성되어 있는지 알아보도록 한다.
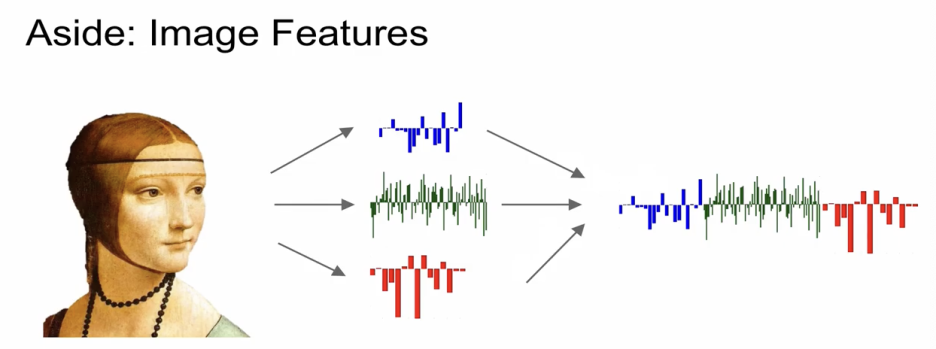
오리지날 이미지에 적용하면 모든 노드를 커버해야해서 복잡하기에,
feature추출 후 linear classifier 적용했다.
- Feature 추출 (호그나 컬러 히스토그램)
- 추출한 여러개의 feature들을 giant column vector처럼 이어주고 linear classifier에 적용.
방법1) Color histogram
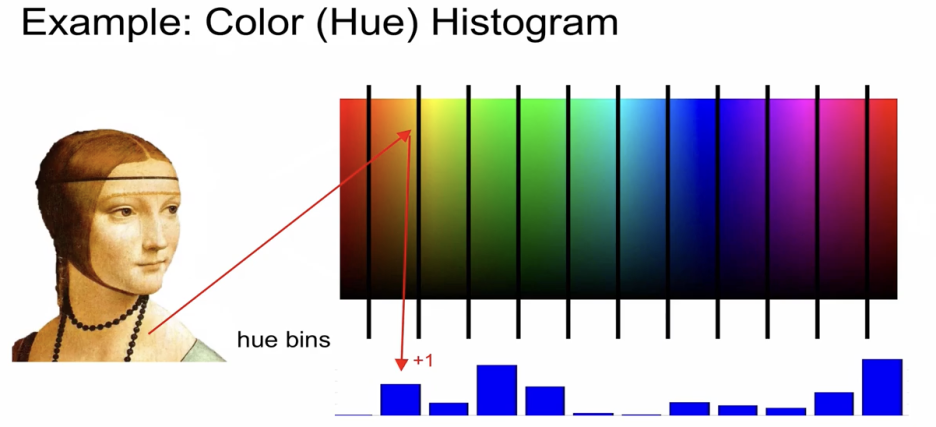
이미지 내의 모든 픽셀들의 색상 파악하고, 전체 컬러 파노라마가 있을 때 각각의 컬러에 해당하는 bin이 몇개인지
이미지 내의 각각의 bin에 해당하는 픽셀들이 몇개인지 카운트하여 feature 추출
방법2) HOG features

edge의 방향 orientation이 feature가 되겠는데, 오른쪽 그림처럼 8*8 pixel이 구성되어 있는 구역을 보면서
edge의 방향을 총 9개로 구성을 해서 9가지 bin에 몇개가 속하는가를 기준으로 해서 edge 의 orientation을 feature로 추출하는 것.
방법3) Bag of Words

왼쪽 이미지의 여러 지점들을 보고, 작은 지점(local patch)들을 vector로 기술하고, 하나로 모아 사전화하고
이 사전 중에서 테스트 할 이미지와 가장 유사하게 생긴 feature vector를 찾는다.(k means방식 사용)
이 feature vector들을 추출하고 linear classify 적용.

과거방식 : feature 추출을 사람이 인위적으로 진행
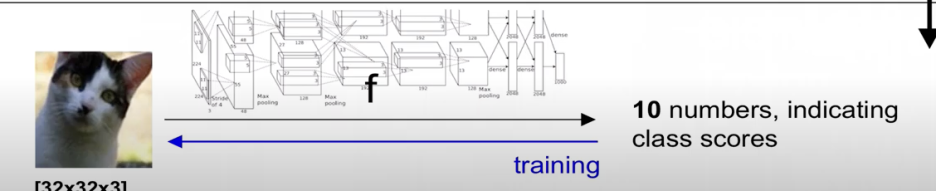
현재방식 : 전통적인 방식과는 다르게 feature 추출을 인위적으로 하지 않고 이미지를 classifier에 적용하면 우리 함수가 알아서 결과값을 출력해주는 방식을 취한다.
즉, feature 추출을 기존 방식에서는 사람이 인위적으로 했다면, 새로운 방식에서는 feature 추출할 필요가 없다.
'7. 수학공부 > 기타' 카테고리의 다른 글
| Lecture 5 Training Neural Networks, Part I (2) | 2024.12.06 |
|---|---|
| Lecture 5 Training Neural Networks, Part I (0) | 2024.12.06 |
| Lecture 4 Introduction to Neural Networks (4) | 2024.12.05 |
| CS231 Lecture 2 | Image Classification (3) | 2024.12.02 |
| CS231N, Lecture 1 | Introduction to Convolutional Neural Networks for Visual Recognition (0) | 2024.11.30 |