CS231n 4강 공부 및 리뷰를 시작하겠습니다. 인공지능을 준비하시는 분들에게도 도움이 되었으면 좋겠습니다.
Backpropagation
Gradient Descent를 구하는 방법은 2가지가 있다.

실제로는 Numerical gradient로 구하면 된다.

매우 간단한 과정으로 나왔는데, 실제 Computational Graph는 굉장히 거대한 규모로 되어있다.
따라서 위의 그림처럼 늘여서 한꺼번에 계산한다는 것은 불가능하다.
아래의 예시 2가지를 보면 불가능한 이유를 알 수 있다.
AlexNet 예시)

Neural Turing Machine + RNN 예시)

위의 두 모듈처럼 매우 거대한 규모이기 때문에 한꺼번에 모두를 계산하는 것은 어렵다.
간단한 예를 들어서 module별로 계산해나가는 방법을 학습해보려 한다.


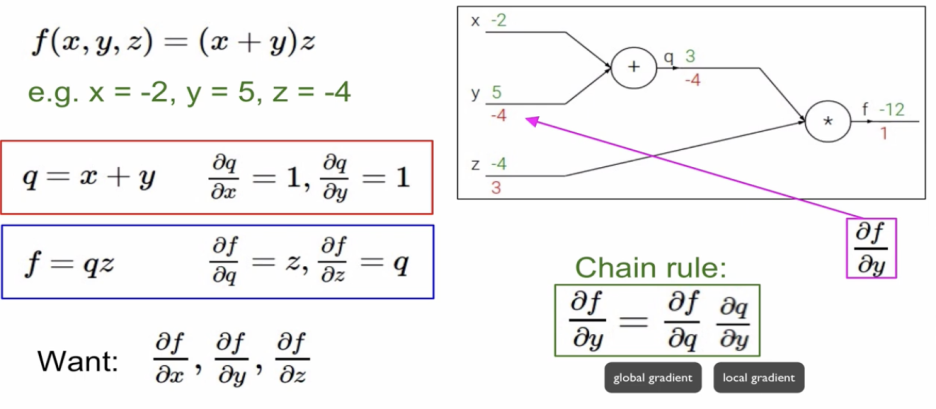
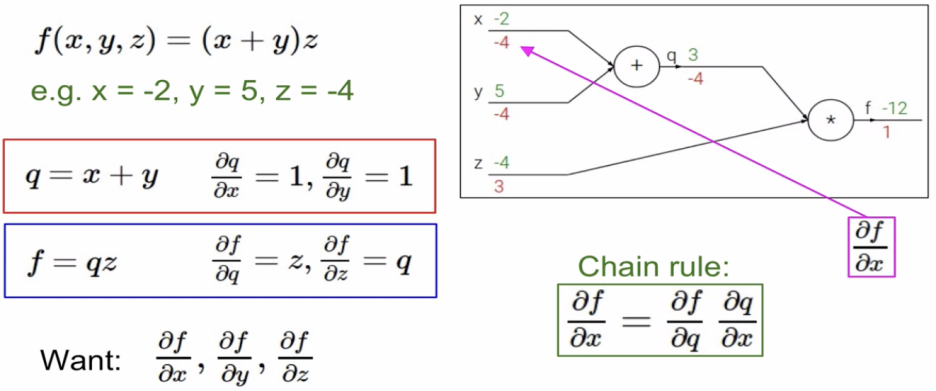
녹색 숫자 : 실제값 / 빨간 숫자 : Gradient 값
간단한 예시를 통해 Gradient를 알아보았다.

Local gradient는 forward pass시에 구해서 메모리에 저장을 해둔다.
Global gradient는 backward pass동안에 구할 수 있다.
또다른 예시,


분모부분을 구한 다음에 마지막에 분모와 분자를 뒤집어주기 위해 1/X한 것인데,
편미분을 이용해서 수식으로 적어보자면 아래와 같다.

x= 1.37 >> 1/-1.37^2이 local gradient
(-1/1.37^2)(1.00) = -0.53이 global gradient




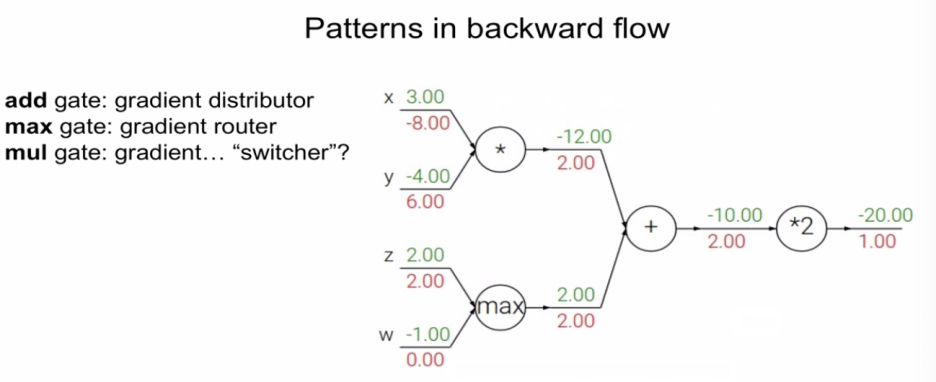
*더하기 연산 : gradient distributor라고 불린다. gradient를 동일한 값으로 전파해주는 것이다.

Input 5개의 값에 대한 gradient를 모두 구했다.

앞에서 했던 함수가 Sigmoid와 거의 유사한 형태를 가지고 있는 것을 알 수 있다.
하지만, Sigmoid function은 미분을 했을 때 굉장히 독특한 특성을 가지고 있다.


sigmoid function을 미분했을 때, 자기 자신으로 표현이 된다.
따라서, 아래 상자를 Sigmoid gate라고 할 수 있다.
0.20을 복잡한 계산으로 했지만,
실질적으로는 global gradient는 1이 되고,
local gradient는 sigmoid function을 미분하면 된다.
정리


forward는 x * y로 계산하고, backward는 사진처럼 계산한다.
예시1) Torch


수많은 layer들이 있고, 레고의 블록을 조립하듯이 layer 한개 한개들을 조립해주는 과정으로 구성
예시2) Caffe Layers

현실적으로 Gradient가 모두 vector라고 가정했을 때를 구해보겠다.


Q: What is the size of the Jacobian matrix ?
A: [4096 X 4096!]
Q: what does it look like?
A:


ASSIGNMENT

Summary

Neural Network(신경망)

input layer인 x에서는 3072개를 가지게 되고
w1(가중치)와 연산되어서 hidden layer는 100개의 node로 구성되고,
다시 w2(가중치)와 연산이 되어서 output layer인 score에서는 10이 된다.
100개의 히든노드 각각이 1개의 피처를 담당한다.
ex) 100개 중 어떤 1개의 히든 노드는 앞쪽을 보고 있는 빨간색의 자동차를 담당하는 노드다. 라고 표현할 수 있다.
노드의 갯수를 몇개로 할 것인지는 실험에 따라서 최적의 값을 구해야 한다.
data driven approach에서
parametric approach : Neural Network(1개의 클래스에 대해 여러개의 classifier가 존재한다.)
non-parametric approach : 대표케이스는 nearest approach(1개의 클래스에 1개의 classifier만 존재한다.)
ASSIGNMENT

Neural Network

cell body : soma
dendrites : input이 들어오는 곳
axon : 연산결과에 따라 output이 나가는 곳
cell body 내에서 단순한 합연산이 이루어진 후, activation function을 적용해서 non linearity를 만들어주고
axon을 통해 다음 뉴런으로 전달한다. (가중치 w0,w1,w2에 의해 각각의 dendrite에서 들어온 data들이 얼마나 영향력을 가지고 있는지 결정하게 된다.)
전통적으로 많이 사랑 받아왔던 함수는 Sigmoid activation funtion이다.
이유 : x가 0일 때, 0.5의 값을 가지면서 x가 아무리 작아져도 y값이 0 이상이 되고, x가 아무리 커지더라도 y값이 1 이하가 된다. 즉, 0과 1사이에 수렴이 되기 때문에 특정 뉴런의 영향력을 0과 1 사이로( 마치 확률처럼) 특정해주기가 쉽기 때문입니다.
주의할 내용

생물학적인 뉴런은 종류가 다양하고, dendrite에서 훨씬 복잡한 non-linear한 연산들을 수행한다. synapse도 단순한 가중치를 가지는게 아니라 복잡하게 갖는다.
따라서, 인공신경망을 실제의 신경망에 비유해서 이야기하는 것에 대해 경계를 해야한다.
Activation Functions

현재 가장 많이 사용하는 것이 ReLU

weight를 가진 것만 layer라 한다.
따라서, input layer는 weight를 가지지 않기 때문에 제거된다.

모든 layer가 연결되어있는 것을 "Fully-connected layers"라 한다.
모든 노드들을 연결하는 것은 효율적으로 계산할 수 있기 때문이다.
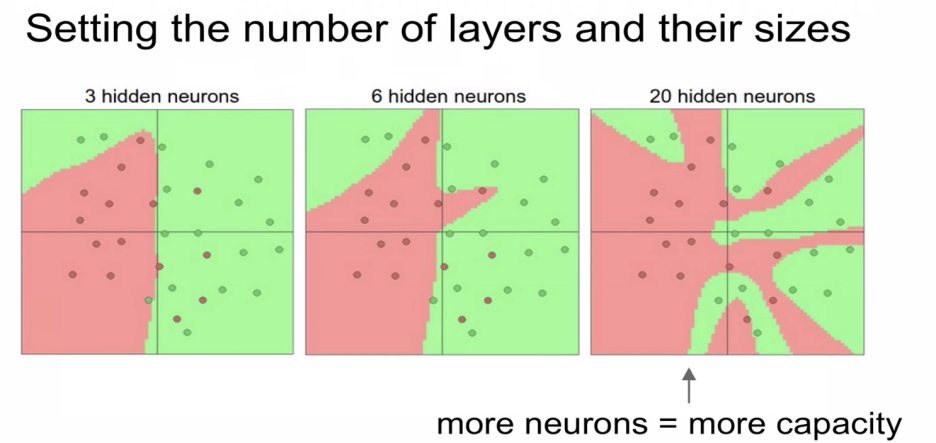
layer의 갯수와 사이즈에 대한 예인데,
많아지면 많아질수록 분류를 하는 능력이 좋아진다.
3개에는 빨간점을 많이 놓치지만 갯수가 증가할 수록 많이 잡는다.

조심해야 할 것은 뉴럴넷의 사이즈가 Regularization역할을 하는 것은 아니다.
일반화를 하기 위해서는, Regularization의 strength를 높여야 한다.

Data의 overfitting이 일어나지 않도록 neural network을 잘 구성하는 옳은 방법은
network을 작게 만드는게 아니라, regularization strength를 높여줘야 한다.
각각의 layer마다 다른 activation function을 쓰는것이 의미있는가? 일반적으로 같은 것을 쓴다.
'7. 수학공부 > 기타' 카테고리의 다른 글
| Lecture 5 Training Neural Networks, Part I (2) | 2024.12.06 |
|---|---|
| Lecture 5 Training Neural Networks, Part I (0) | 2024.12.06 |
| Lecture 3 | Loss Functions and Optimization (1) | 2024.12.03 |
| CS231 Lecture 2 | Image Classification (2) | 2024.12.02 |
| CS231N, Lecture 1 | Introduction to Convolutional Neural Networks for Visual Recognition (0) | 2024.11.30 |