오늘은 MIT GilbertStrang교수님의 Linear algebra 8강에 대해 학습하겠습니다.

Solvability conditions on b

The third row of A is the sum of its first and second rows, so we know that if Ax = b the third component of b equals the sum of its first and second components. If b does not satisfy b3 = b1 + b2 the system has no solution. If a combination of the rows of A gives the zero row, then the same combination of the entries of b must equal zero.
One way to find out whether Ax = b is solvable is to use elimination on the augmented matrix. If a row of A is completely eliminated, so is the corre sponding entry in b. In our example, row 3 of A is completely eliminated:
If Ax = b has a solution, then b3 − b2 − b1 = 0. For example, we could choose b. From an earlier lecture, we know that Ax = b is solvable exactly when b is in the column space C(A). We have these two conditions on b; in fact they are equivalent.
A의 세 번째 행은 첫 번째 행과 두 번째 행의 합이므로, Ax = b이면 b의 세 번째 성분은 첫 번째 성분과 두 번째 성분의 합과 같다는 것을 알 수 있다. b가 b3 = b1 + b2를 만족하지 않으면 해를 가질 수 없다. A의 행들의 조합이 0 행이라면, b의 항목들의 같은 조합은 0과 같아야 한다.
Ax = b 가 해결 가능한지 여부를 알아내는 한 가지 방법은 augmented matrix에서 elimination소거법을 사용하는 것이다. A의 행이 완전히 소거된다면, b의 해당도 마찬가지로 소거된다. 예제에서 A의 3행은 완전히 소거된다.
만약 Ax = b가 해를 갖는다면, b3 - b2 - b1 = 0이다. 예를 들어, 우리는 b를 선택할 수 있다. 앞의 강의를 통해, 우리는 b가 열 공간 C(A)에 있을 때 Ax = b가 정확히 풀린다는 것을 알고 있다. b에 이 두 조건이 있다; Equaivalent (동치)이다.


Complete solution

In order to find all solutions to Ax = b we first check that the equation is solvable, then find a particular solution. We get the complete solution of the equation by adding the particular solution to all the vectors in the nullspace.
Ax = b의 모든 해를 구하기 위해서 먼저 풀 수 있는 방정식인지 확인한 다음 특정 해를 구한다. nullspace(영공간)의 모든 벡터에 특정 해를 더함으로써 방정식의 완전한 해를 얻는다.
- A particular solution

One way to find a particular solution to the equation Ax = b is to set all free variables to zero, then solve for the pivot variables.
For our example matrix A, we let x2 = x4 = 0 to get the system of equa tions:
which has the solution x3 = 3/2, x1 = −2. Our particular solution is: z
방정식 Ax = b에 대한 특정 해를 구하는 한 가지 방법은 모든 자유 변수를 0으로 설정한 다음 피벗 변수를 해결하는 것이다.
- Combined with the nullspace

The general solution to Ax = b is given by xcomplete = xp + xn, where xn is a generic vector in the nullspace.
Ax = b에 대한 일반적인 해는 xcomplete = xp + xn으로 주어지는데, xn은 nullspace에서의 일반 벡터이다.

Rank
The rank of a matrix equals the number of pivots of that matrix. If A is an m by n matrix of rank r, we know r ≤ m and r ≤ n.
행렬의 순위는 해당 행렬의 피벗 수와 같다. 만약 A가 m x n 행렬 r이라면, r ≤ m이고 r ≤ n임을 알 수 있다.

- Full column rank
If r = n, then from the previous lecture we know that the nullspace has dimension n − r = 0 and contains only the zero vector. There are no free variables or special solutions.
If Ax = b has a solution, it is unique; there is either 0 or 1 solution. Examples like this, in which the columns are independent, are common in applications.
r = n이면 앞 강의를 통해 nullspace가 dimension n - r = 0이고 zero vector만 포함한다.
free variations나 special solutions가 없음을 알 수 있다.
Ax = b에 해가 있으면 유일하다. 해가 0 또는 1 이다. 이와 같은 열이 독립적 예시는 applications에서 흔히 볼 수 있다.
- Full row rank
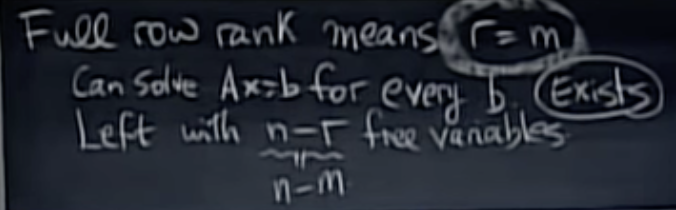
If r=m,thenthereducedmatrixR=[ I F ] hasnorowsofzerosandso there are no requirements for the entries of b to satisfy. The equation Ax = b is solvable for every b. There are n − r = n − m free variables, so there are n − m special solutions to Ax = 0.
r=m이면, 감소된 행렬 R=[ I F ]는 0의 행이 없으므로 b의 항목을 만족시킬 필요가 없다. 식 Ax = b는 모든 b에 대해 풀 수 있다. n - r = n - m 자유 변수가 있으므로 Ax = 0에 대해 n - m special solutions가 있다.
- Full row and column rank
If r = m = n is the number of pivots of A, then A is an invertible square matrix and R is the identity matrix. The nullspace has dimension zero, and Ax = b has a unique solution for every b in Rm.
만약 r = m = n이 A의 피벗의 수이라면, A는 invertible square matrix이고 R은 identity matrix이다. nullspace 차원은 0이고, Ax = b는 Rm의 모든 b에 대해 유일한 해를 갖는다.
- Summary
