안녕하세요 오늘은 7강 Solving Ax = 0: Pivot Variables, Special Solutions Space and Nullspace에 대해 배우겠습니다.

Solving Ax = 0: pivot variables, special solutions
* Number of piviots = Rank of A
The nullspace of a matrix A is made up of the vectors x for which Ax = 0.
행렬 A의 nullspace는 Ax = 0인 벡터 x로 구성된다. (중요한 점은 A행렬은 독립적이지 않다.)
our algorithm for computing the nullspace of this matrix uses the method of elimination, despite the fact that A is not invertible. We don’t need to use an augmented matrix because the right side (the vector b) is 0 in this computation.
The row operations used in the method of elimination don’t change the solution to Ax = b so they don’t change the nullspace. (They do affect the column space.)
Null space를 구하는 방법은 elimination(소거)하는 것이다, 중요한 점은 elimination하는 과정에서 Null space를 변화시키지 않는다는 것이다. Column space에는 영향을 미치겠지만, 결과적으로 Null space는 변경되지 않는다.

Column 2에 존재해야할 pivot이 없는 것은 Column1에 dependent하기 때문이며, 두 column이 같은 선상에 위치한다는 뜻입니다.
The matrix U is in echelon (staircase) form. The third row is zero because row 3 was a linear combination of rows 1 and 2; it was eliminated.
The rank of a matrix A equals the number of pivots it has. In this example, the rank of A (and of U) is 2.
행렬 U는 사다리꼴(계단형) 형태이다.
행렬A의 pivot수는 2개이며, 이 말은 A의 rank는 2라는 뜻이다.
Special solutions
Once we’ve found U we can use back-substitution to find the solutions x to the equation Ux = 0
U를 찾은 후에는 역 substit 방정식을 사용하여 Ux = 0에 대한 해 x를 찾을 수 있다.

Back substitution과정을 진행한다.
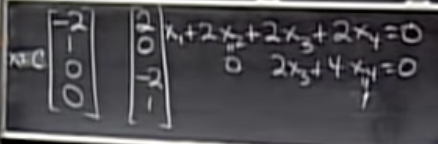
The nullspace of A is the collection of all linear combi nations of these “special solution” vectors.
A의 nullspace는 "special solution" 벡터들의 모든 선형 조합들의 집합이다.

The rank r of A equals the number of pivot columns, so the number of free columns is n − r: the number of columns (variables) minus the number of pivot columns. This equals the number of special solution vectors and the dimension of the nullspace.
free variable은 pivot을 제거한 나머지 column 수가 될 것이다. ( 다시말하면, column - rank )

따라서, n-r인 column 4에서 rank 2를 빼면 최종 free variable은 2가 된다.
Reduced row echelon form
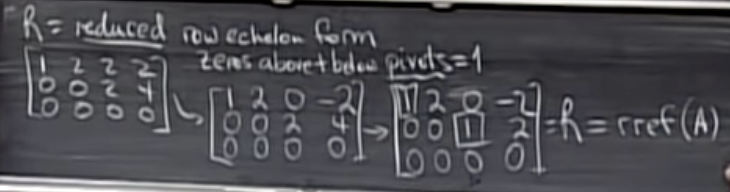
By continuing to use the method of elimination we can convert U to a matrix R in reduced row echelon form (rref form), with pivots equal to 1 and zeros above and below the pivots.
제거 방법을 계속 사용함으로써 U를 reduced row echelon form(rref 형태)의 행렬 R로 변환할 수 있으며, pivot은 1이고pivot 원소들의 아래,위로 모두 0이 된다.
* pivot 원소들은 반드시 1이어야 하고, pivot 변수의 모든 아래/위 행렬은 0이 되어야 한다.

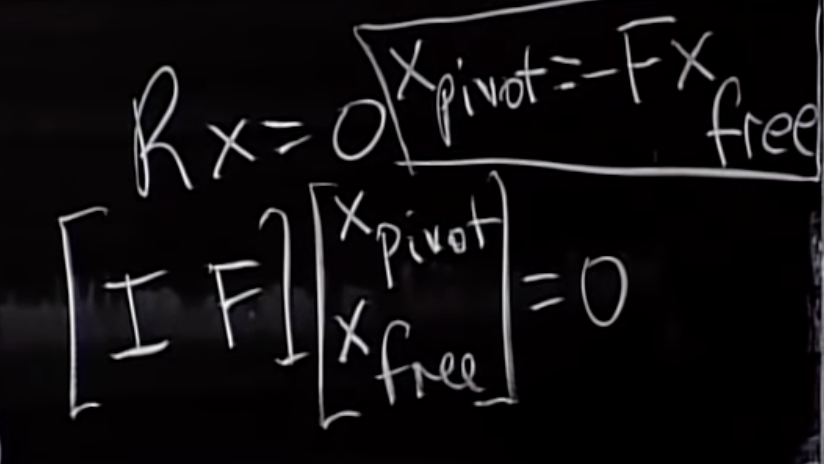

행렬 U를 소거하여 만들어낸 Rx=0 해도 동일한 Null space에 존재하지 않는다.
이는 행렬을 A에서 R로 변화시키면서, 각 행렬의 column space가 변했을지 모르지만 고유한 성질은 변하지 않는다는 것을 나타내며, 동일한 공간(Null space)에 존재하게 된다.